<..> mat_rozszerzona:

	7
Wyznacz najmniejszą i największą wartość funkcji f(x)=		na przedziale <0,6>
	√3x2 −12x+13

Tadeusz: − dziedzina − analizuj wyrażenie pod pierwiastkiem (sprawdź gdzie ma minimum) x_w tego wyrażenia wyznaczy maximum f(x) − dalej oczywista oczywistość −

aaaa:(: dziedzina mi wyszła x∊R , a Tobie jak? z kolei potem poleciałem że min wartość to będzie x_w on mi wyszedł 2, a w(2)=1. Ja nie pomagam a pytam bo sam nie wiem

Tadeusz: ... i ok−

mat_rozszerzona: czyli mam liczyć tak jak szukam min i max funkcji kwadratowej na przedziale <0,6> tylko ,że w odpowiedzi wziąć że max=min, a min=max?

aaaa:(: hmm moje kroki są takie: D: √3x²−12x+13>0 /² z tego: Δ<0 zatem D: x∊R skoro wiem, że funkcja jest nad osią OX i ramiano ma skierowane do góry, to f_min będzie w x_w. x_w=2 w(2)=1 i trochę blokada, nie potrafię robić oczywistych oczywistości, mógłbyś Tadeuszu rozpisać to łopatologicznie?

aaaa:(: _w czyli te wartość min mieście się w przedziale <0,6> tak? a ta wartość max jaka będzie?

Draghan: A wartość maksymalna będzie pewnie w którymś z końców przedziału...

aaaa:(: jak obliczyłem sobie funkcję f biorąc sobie skrajne liczby z przedziału to: w(0)=13 w(6)=49 czyli odpowiedzią jest 49?

Tadeusz: ... czyli wiesz już, że wyrażenie pod pierwiastkiem (mianownik) przyjmuje wartość najmniejszą dla x=2 Wartość ta to 1. Wtedy f_max=7 Pozostaje do policzenia f(0) i f(6) i wyznaczenie wartości najmniejszej w określonym przedziale.

aaaa:(: Hmmm, a można wytłumaczyć dlaczego gdy znamy dla jakiego x mamy najmniejszą wartość, to, to... nie rozumiem tego przejścia że wtedy f_max=7

Draghan:

	7
Ponieważ funkcja to nie samo wyrażenie kwadratowe, a f(x) =
	(...)

aaaa:(:

	7
aaaaa, czyli potem f(x)=		=7
	1

	7		1
kolejno fmin=		=		?
	49		7

tylko jeszcze pytanko, bo Draghan Twoja ostatnia wypowiedź odnosi się do tego że f{max}=7 tak? a dlaczego tak jakby zamieniamy skoro tam było f_min to w ogólnej funkcji jest f_max ?

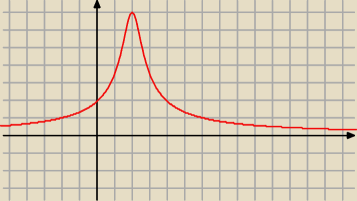
5-latek: Taki jest wykres tej funkcji

Tadeusz: ...a kiedy wartość ułamka przy stałym liczniku ma wartość największą ?

aaaa:(: o to teraz to już nic nie wiem haha

zawodus: dopiero wczoraj robiłeś ode mnie takie zadanko

5-latek:

	7
A ktory ulanek bedzie wiekszy np		czy 72 ?
	1

Wiec popatrz na mianowniki i wyciagaj wnioski

Draghan: aaaa: ), im większy mianownik, tym mniejsza liczba Ale ja już stąd idę, masz tutaj zdolniejszych ludzi do pomocy Miłego dnia!

Draghan: Przepraszam, 5−latek, nie widziałem Twojej wiadomości

aaaa:(:

	7
ułamek		jest większy xd
	1

zawodus wiem, ale trochę inne i już dupa ...

5-latek: A czemu przepraszasz ? Ciekawe czy juz zajarzyl

aaaa:(: no własnie chyba nie zajarzył

Draghan: Przepraszałem dlatego, że odpowiedziałem (pośrednio) na Twoje pytanie, które było skierowane do aaaa: ), żeby się czegoś sam(a) nauczył(a)

aaaa:(: ja trochę się pogubiłem o co tu już chodzi

Draghan: To po kolei i niespiesznie Najpierw spójrz, co masz dane i co masz policzyć Później zobacz, co policzyłeś ...?

aaaa:(: więc tak: x_w=2 wartość = 1 potem skrajne liczby z przedziału mamy: w(0)=13 w(6)=49 pytanko, dlaczego zamienialiśmy f_min na f_max tej całej funkcji jak wyznaczyć w takim razie nasze f_min pewnie to już było powiedziane, ale ja niestety nie skumałem co mnie trochę dołuje

Draghan: Nie dołuj się Wystarczająco wiele dziur mamy na drogach Mamy wartości f{_min} i f_max, ale nie dla Twojej funkcji, której wzór masz dany w zadaniu Tylko dla mianownika we wzorze tej funkcji A im większy mianownik, tym mniejsza liczba Teraz zaczyna świtać?

Draghan: Coś mi nie pykło w f_min

aaaa:(:

	7
aaaa czyli fmin=		? ?
	13

Draghan: Okej, to jeszcze inaczej Masz policzone dla mianownika trzy wartości. 1) 1 2) 13 3) 49 Wybierz minimalną i maksymalną

aaaa:(: no to max: 1 min: 13 xd?

Draghan: Eeeeee... Nie Minimalna wartość mianownika to 1, a maksymalna to 49 Teraz wstawiasz to do wzoru funkcji i otrzymujesz...?

Draghan: Znaczy nie stricte do wzoru jako za iksa, tylko wiadomo, za cały mianownik

aaaa:(:

	1
7 i
	7

Draghan: Wrrrróć...! Co mamy w mianowniku? Patrzę, patrzę... A tam pierwiastek z trójmianu kwadratowego Także ten, Ty policzyłeś... Że 1 i że 49 to są ekstrema w zadanym przedziale z tej funkcji kwadratowej...

	7
Ale mamy f(x) =
	√funkcja kwadratowa

A więc musisz podstawić...

	7
1) a =
	√1

	7
1) b =
	√49

Tak to widzę ja, ale ja nie jestem dobry z matmy

aaaa:(: czyli tak ja Drahan powiedział tak jest git?