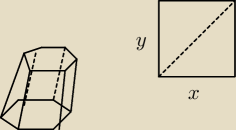
aa Hugo: wśród wszystkich graniastosłupów prawidłowych sześciokątnych w których suma długości wszstkich krawędz jest równa 24 jest taki który ma największe pole powierzchni bocznej. Oblicz długosć krawędzi podstawy tego graniastosłupa suma krawędzi = 24 Suma kr. podstawy = 6 *2 =12 Suma kr. ścian bocznych = 6 24= 12k.p. + 6 k.b 4=2kp + kb I teraz jak to pokazać ze kwadratowe sciany graniastosłupa będą naj obszerniejsze Myślałem coś o f. kwadratowej

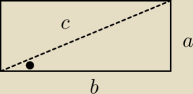Hugo: a coś takiego ? sin osiąga największą wartość 1 dla kąta 45 stopni i aby to osiągnąć musi być kwadrat

Hugo: Wtedy: 24= 12k.p. + 6 k.b k.p=k.b 24 = 18kr

	1
kr= 1
	3

Hugo: miałem racje z f kwadratową.. a=1

Janek191: a − długość boku sześciokąta foremnego h − wysokość graniastosłupa prawidłowego sześciokątnego Mamy 12 a + 6 h = 24 / : 6 2a + h = 4 ⇒ h = 4 − 2a oraz pole powierzchni bocznej graniastosłupa P_b = 6a*h = 6a*( 4 − 2a) = 24 a − 12 a² P_b(a) = − 12 a² + 24 a − 12 < 0 ,więc funkcja kwadratowa P_b przyjmuje największą wartość dla

	−24
a = p =		= 1
	2*(−12)

Wtedy h = 4 − 2*1 = 2 Odp. a = 1 =========== spr. 12*1 + 6*2 = 12 + 12 = 24 −−−−−−−−−−−−−−−−−−−−−−−−−