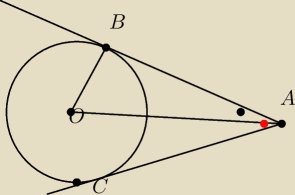
 Oblicz miarę kąta miedzy stycznymi do okręgu x2+y2+2x−2y−3=0 poprowadzonymi przez punkt
A=(2,0)
Więc: Obliczę ten trójkąt A,O,B następnie z twierdzenia cosinusów kąt OAB i przemnoże razy dwa
by otrzymać kąt CAB
równanie okręgu: x2+y2+2x−2y−3=0
x2+2x+4+y2−2y+4−8 −3=0
(x+2)2 + (y−2)2 = 12
środek okręgu −> O (−2,2)
Odlgełość AO = √((2−−2)2 + (0−2)2)
√16+4 = √20= 2√5
r=√12
z tw pitagorasa
12 + |AB|2 = 20
|AB| = 2√2
Z tw cosinusów
|BO|2 = |BA|2 + |OA|2 − 2|BA|*|OA|cosα
8=20+12− 2* √20*√12*cosα
−24=− 2* √20*√12*cosα
12=√20*√12*cosα
12=*√240*cosα
3= √15cosα
Oblicz miarę kąta miedzy stycznymi do okręgu x2+y2+2x−2y−3=0 poprowadzonymi przez punkt
A=(2,0)
Więc: Obliczę ten trójkąt A,O,B następnie z twierdzenia cosinusów kąt OAB i przemnoże razy dwa
by otrzymać kąt CAB
równanie okręgu: x2+y2+2x−2y−3=0
x2+2x+4+y2−2y+4−8 −3=0
(x+2)2 + (y−2)2 = 12
środek okręgu −> O (−2,2)
Odlgełość AO = √((2−−2)2 + (0−2)2)
√16+4 = √20= 2√5
r=√12
z tw pitagorasa
12 + |AB|2 = 20
|AB| = 2√2
Z tw cosinusów
|BO|2 = |BA|2 + |OA|2 − 2|BA|*|OA|cosα
8=20+12− 2* √20*√12*cosα
−24=− 2* √20*√12*cosα
12=√20*√12*cosα
12=*√240*cosα
3= √15cosα
| 3√15 | ||
cosα= | ||
| 15 |
| 3√15 | 3√15 | |||
i teraz niby cos2α = cos2α−sin2α= cos2 | − sin2 | // z jedynki tryg | ||
| 15 | 15 |
| 3√15 | 3√15 | |||
cos2 | +cos2 | + 1 = I jak dalej  ? ? | ||
| 15 | 15 |
 dostaniesz jabłuszko ICSP
dostaniesz jabłuszko ICSP 

 wzory skróconego mnozenia znam r2=11
wzory skróconego mnozenia znam r2=11



 ... ciekawe grze jest Mila
... ciekawe grze jest Mila

 to wy sie znacie ! Proszę koniecznie pozdrowić moją Mentorke !
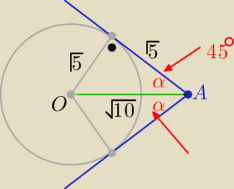
Skoro mamy długosci √5. √5, oraz √10 to jest to trójkąt równoramienny prostokątny ⇔ α=45
zatem α+α=90 stopni !
dz
to wy sie znacie ! Proszę koniecznie pozdrowić moją Mentorke !
Skoro mamy długosci √5. √5, oraz √10 to jest to trójkąt równoramienny prostokątny ⇔ α=45
zatem α+α=90 stopni !
dz  !
gdzie ∫(dz) ∊= {dziękuję}
!
gdzie ∫(dz) ∊= {dziękuję}


| √5 | |||||||||||
sinα= | ⇒α=45o | ||||||||||
|

| √5 | √2 | |||
sinα= | = | |||
| √10 | 2 |
