Pytanie o kartę wzorów Blue: Czy wzór na ilość przekątnych w wielokącie jest w karcie wzorów maturalnych

bezendu: nie ma

razor: nie ma, ale jest łatwy sposób żeby go wyprowadzić podchodzi trochę pod kombinatorykę mając wielokąt o n wierzchołkach chcemy się dowiedzieć ile ma przekątnych. wybieramy 2

	n 2
wierzchołki na		sposobów i tworzymy odcinki − wśród tego są wszystkie przekątne jak i

wszystkie boki − więc odejmujemy ilość boków n

n 2		n(n−1)		n(n−1) − 2n		n(n−3)
	− n =		− n =		=
		2		2		2

Blue: kurcze, tylko nie miałam jeszcze kombinatoryki i nie za bardzo rozumiem ten zapis w nawiasie

5-latek: https://matematykaszkolna.pl/strona/1014.html

razor: piszesz maturę i nie robiłaś jeszcze kombinatoryki?

Saizou : można to na chłopski rozum wziąć z jednego wierzchołka wychodzi n−1 przekątnych (bo sam do siebie nie wyjdzie) takich wierzchołków mamy n, czyli n(n−1), ale liczymy przekątne 2 razy (np. z wierzchołka A do B oraz z B do A ), dlatego dzielmy przez 2

	n(n−1)
d=
	2

Blue: hmmm... dzięki, ale chyba jednak będę musiała nauczyć się tego wzoru na pamięć

Blue: Saizu Twój sposób bardziej do mnie przemawia

Blue: *Saizou

Blue:

	n(n−1)		n(n−3)
ale to w końcu jaki jest ten wzór?		czy
	2		2

Piotr 10: no ten drugi , ten pierwszy to tyczy sie liczyb powitań

zawodus:

n(n−3)
2

Blue: Powitań?

zawodus: liczba powitań

n 2		n(n−1)
	=
		2

Piotr 10: tak

zawodus: 10 osób gra w szachy w na zawodach. Każdy gra z każdym dokładnie raz. Oblicz ile partii będzie w tym turnieju?

10 2		n(n−1)
	=		=45
		2

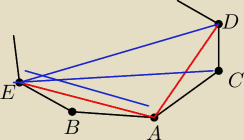
Saizou : a no tak, coś pomyliłem xd przecież z A wychodzi n−3 przekątnych, bo nie idzie do A,B,C przepraszam za błąd ale jak tamto pisałem byłem myślami gdzie indziej wiec

	n(n−3)
d=
	2