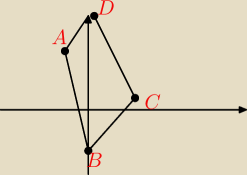
 Cześć ; )
Mam małą wątpliwość. Mianowicie, wydaje mi się, że zadanie zrobiłem dobrze, ale w odpowiedziach
jest inny wynik.
Dane są punkty A(−2;5), B(0;−3) i C(4;1). Wyznacz punkt D tak, aby czworokąt ABCD był
równoległobokiem i oblicz pole tego czworokąta.
Rysunek wybitnie poglądowy, miał być to równoległobok, ale w tym edytorze rysowanie to dla mnie
prawdziwa katorga. Wracając do zadania:
Aby był to równoległobok wektory AD i BC muszą być sobie równe:
AD=[x+2;y−5]
BC=[4;4]
[x+2;y−5]=[4;4]
x+2=4
x=2
y−5=4
y=9
D(2;9)
Mam wszystkie współrzędne punktów, więc pole mogę policzyć jako dwa pola trójkątów: ABC i ACD.
Mam dane wierzchołki, więc pola mogę liczyć ze wzoru z tablic:
Cześć ; )
Mam małą wątpliwość. Mianowicie, wydaje mi się, że zadanie zrobiłem dobrze, ale w odpowiedziach
jest inny wynik.
Dane są punkty A(−2;5), B(0;−3) i C(4;1). Wyznacz punkt D tak, aby czworokąt ABCD był
równoległobokiem i oblicz pole tego czworokąta.
Rysunek wybitnie poglądowy, miał być to równoległobok, ale w tym edytorze rysowanie to dla mnie
prawdziwa katorga. Wracając do zadania:
Aby był to równoległobok wektory AD i BC muszą być sobie równe:
AD=[x+2;y−5]
BC=[4;4]
[x+2;y−5]=[4;4]
x+2=4
x=2
y−5=4
y=9
D(2;9)
Mam wszystkie współrzędne punktów, więc pole mogę policzyć jako dwa pola trójkątów: ABC i ACD.
Mam dane wierzchołki, więc pola mogę liczyć ze wzoru z tablic:
| 1 | ||
PΔABC= | |(xB−xA)(yC−yA)−(yB−yA)(xC−xA)| | |
| 2 |
| 1 | 1 | |||
PΔABC= | |2*(−4)−(−8*6)|= | |−8+48|=20(j)2 | ||
| 2 | 2 |
| 1 | ||
PΔACD= | |(xC−xA)(yD−yA)−(yC−yA)(xD−xA)| | |
| 2 |
| 1 | ||
P= | |6*4−(−4*4)|=20(j)2 | |
| 2 |
 !
!

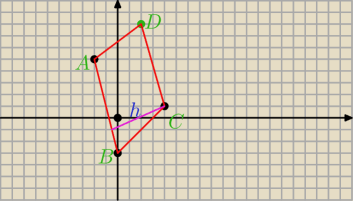 h wysokosc rownolegloboku (czyli odlegloscv punktu C od prostej AB
AB =a dlugosc boku
P=a*h
Punktu D nie liczylem ale chyba cos zle wyliczony bo rysunek krzywy
h wysokosc rownolegloboku (czyli odlegloscv punktu C od prostej AB
AB =a dlugosc boku
P=a*h
Punktu D nie liczylem ale chyba cos zle wyliczony bo rysunek krzywy

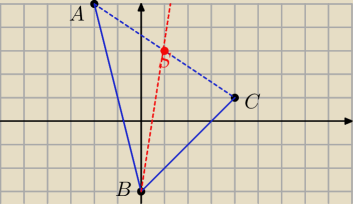 II sposób
Dane są punkty A(−2;5), B(0;−3) i C(4;1).
W równoległoboku przekatne dzielą sie na połowy
II sposób
Dane są punkty A(−2;5), B(0;−3) i C(4;1).
W równoległoboku przekatne dzielą sie na połowy
| −2+4 | 5+1 | |||
S= | , | )=(1,3) środek przekątnej | ||
| 2 | 2 |
| 0+x | ||
1= | ⇔x=2 | |
| 2 |
| y+(−3) | ||
3= | ⇔y=9 | |
| 2 |
 D=(2,9) − też potwierdzony dokładną konstrukcją
D=(2,9) − też potwierdzony dokładną konstrukcją 


