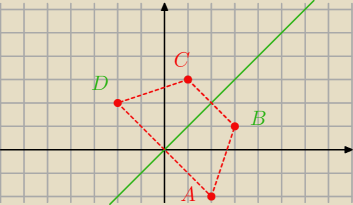
Punkty B=(3;1), D=(-2;2) są przeciwległymi wierzchołkami miri: Punkty B=(3;1), D=(−2;2) są przeciwległymi wierzchołkami trapezu równoramiennego ABCD, w którym AB∥CD. Prosta o równaniu y=x jest osią symetrii tego trapezu. Oblicz współrzędne wierzchołków A i C oraz pole tego trapezu. Pomocy, wychodzą mi szalone wyniki :

Marcin:

Marcin: A i C zamień miejscami. żeby AB||CD

miri: A i C powinny być na odwrót z treści zadania, ale to na marginesie

Marcin: Przecież się poprawiłem

miri: Musieliśmy dodać w tym samym czasie

miri: UPP

Marcin: Dalej nie wiesz? Myślałem że już po problemie

miri: Odpowiedzi dalej wychodzą złe... jakieś 6 i −6, nie wiem gdzie robie błąd z resztą rysunek miałam od początku dobry

Marcin: No to hmm Policz odległość punktu D od prostej (oś symetrii) Dodatkowo wiesz, że prosta która zawiera DA, jest prostopadła do tej prostej, która jest osią symetrii. Kombinuj dalej. Jak coś, to pomogę

zawodus: Marcin możesz już zajrzeć do maturki przygotowanej prze ze mnie Miałem problem z wyborem zadań, tyle jest godnych uwagi

miri: obliczyłam to, wyznaczyłam dwie proste prostopadłe do danej przechodzące przez podstawy, robiłam wszystko ze wzorami na odległość pkt od prostej i długość odcinka i głupoty wychodzą

Marcin:

Marcin: Wyznasz punkt przecięcia się prostej zawierającej oś symetrii i prostej zawierającej punkty D i A. Na rysunku widać, że ma być to (0,0 Ty to wylicz.