Bardzo ambitne zadanie maturzystka : Znalazłam bardzo bardzo ambitne zadanie z rozszerzonej matury sierpniowej z 2013r. Treść: Punkty A=(1,3) i D=(2,1) są wierzchołkami trapezu ABCD o podstawach AB i CD. Wierzchołki B i C leżą na osi Ox, a ramię BC tego trapezu ma długość 2. Wyznacz równania prostych AB i CD. Jak to rozwiązać? Męczę się już nad tym 2,5 godziny

Tyrmand: ale w sierpniu przecież nie ma rozszerzenia...

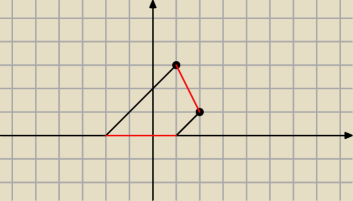
Marcin: Mała podpowiedz rysunkowa To jest jedna opcja, bo jest jeszcze druga.

maturzystka : zadanie znalazłam tutaj na stronie w zadaniach z matury, gdzie jest napisane że jest to z matury rozszerzonej z sierpnia 2013r., może błąd autora strony? to nieistotne.. interesuje mnie rozwiązanie zadania

Marcin: Chociaż nie, ten rysunek może wprowadzić w błąd

Marcin: Proste które tworzą podstawy, mają taki sam współczynnik kierunkowy. (są do siebie równoległe)

Piotr 10: Najlepiej to zrobić a₁=a₂

	yb − ya
gdzie a=
	xb − xa

Potem jeszcze masz dlugosc i podstawic cos i tyle

Marcin: Nie każdy zna wzór na współczynnik kierunkowy

maturzystka : nie rozumiem @Piotr 10 skąd ci się to wzięło

Tyrmand: jeśli chodzi o ten wzór to on jest w tablicach

Piotr 10: Marcin Mój wzór jest w tablicach, tylko w innej postaci a=tgα.

kyrtap:

	yb −ya		yb −ya
maturzystka wzór na prostą jest y − ya =		(x − xa) gdzie a =
	xb−xa		xb−xa

Marcin: No tak. Tylko że nie każdy to widzi Może się czepiam, sorry

kyrtap: nie wiem ja się tego wzoru wykułem w pierwszej klasie gdy pani od razu go podała

Marcin: Widziałeś kiedyś wykres logarytmiczny? Znasz dziedzinę logarytmu?

Marcin: O ja, nie tu to miałem wpisać

maturzystka : ja się poddaję, kompletnie nie rozumiem tego zadania

kyrtap: Marcin na kilka frontów

Marcin: Wyznacz równania tych dwóch prostych które tworzą podstawy. Są one do siebie równoległe i znasz punkty przez które przechodzą.

Marcin: żebyś kyrtap wiedział

maturzystka :

	−3
Używając tych magicznych wzorów doszłam do czegoś takiego: a=		oraz a={−1}{xc −2}
	xb −1

co do przyrównaniu dało mi −3x_c +6=−x_b +1

	⎧	xb −xc=2
Potem ułożyłam układ równań	⎩	−3xc +6=−xb +1	oraz druga opcja k{xb −xc=−2

&−3x_c +6=−x_b +1}

	3		1		7
Z pierwszego układu wyszło mi że C(		,0) i B (−		,0) a z drugiego układu C(		,0)
	2		2		2

	11
i B(		,0).. Jak już mam te punkty to już z górki, mam nadzieję że mi dobrze wyszło,
	2

dzięki za pomoc

Mila: Mam takie same wyniki. (punkty: B i C)