plani aaaa:(: W trójkąt abc którego kąt acb ma miarę 60, wpisano okrąg o środku s. Odległość punktu S od wierzchołka A wynosi 10, a od wierzchołka B jest równa 10√3/ Oblicz długość boku AB help

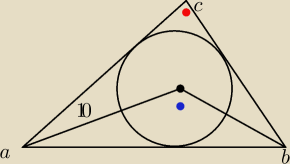
aaaa:(: to czerwone to kąt 60 stopni. jaki kąt jest na tym niebieskim kółeczku? plus proszę o wyjaśnienie dlaczego

Hugo: Z tw cosinusów i poszukaj sb czy czasem to nie ma 120 stopni ten kąt.

aaaa:(: no własnie ten kąt ma 120 stopni, gdy będe wiedział jak sprawdzić wartość tego kąta jestem w domu

Hugo: Z twierdzenia

aaaa:(: ale jak, skoro mam tylko 2 boki i 2 niewiadome

Hugo: http://www.matmana6.pl/tablice_matematyczne/liceum/figury_plaskie_planimetria/13-katy_w_okregu

aaaa:(: no znam to twierdzenie, ale właśnie średnio to widzę na tym przykładzie akurat

aaaa:(: to jak to w koncu z tym jest? potrafi ktoś poiedzieć? bardzo bym prosił

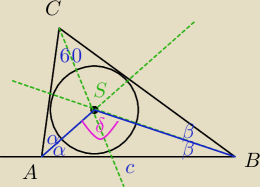
Mila: Srodek okręgu wpisanego w trójkąt leży na przecięciu dwusiecznych katów wewnętrznych trójkata. W ΔABC: 2α+2β+60 =180^o suma kątów w Δ⇔ 2α+2β=120⇔ α+β=60 W ΔABS: α+β+δ=180⇔60+δ=180 δ=120^o Z tw. cosinusów : c²=10²+(10√3)²−2*10*10√3cos(120⁰) dokończysz?

aaaa:(: taaaaaak, bardzo Ci dziękuję! mega rozpisane z tymi kątami! śliczne dzięki

Mila: