Stereometria
jakubs: Trójkąt ostrokątny równoramienny obracamy dookoła podstawy. Objętość otrzymanej bryły oznaczamy
przez V1, a pole powierzchni całkowitej przez P1. Następnie ten sam trójkąt obracamy dookoła
prostej przechodzącej przez wierzchołek trójkąta i równoległej do podstawy. Objętość
otrzymanej w tym przypadku bryły oznaczamy przez V2, a pole powierzchni całkowitej przez P2.
Jeżeli trójkąt obrócę dookoła podstawy to otrzymam : dwa stożki tak ?
Jak narysować dalszą część : Następnie ten sam trójkąt obracamy dookoła prostej przechodzącej
przez wierzchołek trójkąta i równoległej do podstawy. ?
1 maj 14:07
zawodus: "przechodzącej przez wierzchołek trójkąta i równoległej do podstawy." − ten zapis nie określa
jednoznacznie jak obracamy.
1 maj 14:09
Marcin:
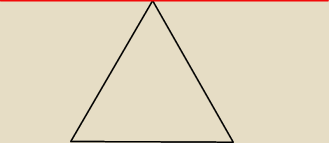
Według mnie to jest prosta równoległa do podstawy, przechodząca przez wierzchołek.
1 maj 14:11
jakubs:
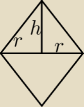
Pierwszy rysunek, czyli obracam wokół podstawy 2r.
1 maj 14:14
bezendu:
Zaczęło się

1 maj 14:16
zawodus:
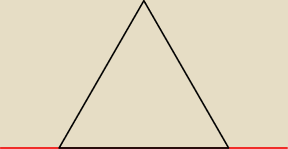 Marcin
Marcin
czerwona prosta też jest równoległa do podstawy i przechodzi przez wierzchołek

1 maj 14:17
jakubs:
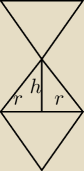
Coś takiego ?

1 maj 14:26
dero2005:
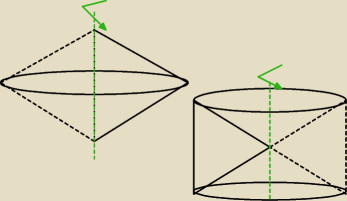
1 maj 15:54
Marcin: zawodus, ale moja też się zgadza, nie?

1 maj 15:56
jakubs: Czyli to mają być dwie osobne figury tak ?
1 maj 15:58
dero2005:
Napisz całą treść zadania
1 maj 16:05
jakubs: dero cała treść brzmi :
Trójkąt ostrokątny równoramienny obracamy dookoła podstawy. Objętość otrzymanej bryły oznaczamy
przez V
1, a pole powierzchni całkowitej przez P
1. Następnie ten sam trójkąt obracamy dookoła
prostej przechodzącej przez wierzchołek trójkąta i równoległej do podstawy. Objętość
otrzymanej w tym przypadku bryły oznaczamy przez V
2, a pole powierzchni całkowitej przez P
2.
| | P2 | |
b) Wykaż, że 1< |
| <1+√2 |
| | P1 | |
1 maj 16:08
dero2005:
Trzeba policzyć V1 i P1 pierwszej figury potem to samo drugiej figury
1 maj 16:13
jakubs: Ok dzięki będę walczył

1 maj 16:15
 Według mnie to jest prosta równoległa do podstawy, przechodząca przez wierzchołek.
Według mnie to jest prosta równoległa do podstawy, przechodząca przez wierzchołek.
 Pierwszy rysunek, czyli obracam wokół podstawy 2r.
Pierwszy rysunek, czyli obracam wokół podstawy 2r.

 Marcin
czerwona prosta też jest równoległa do podstawy i przechodzi przez wierzchołek
Marcin
czerwona prosta też jest równoległa do podstawy i przechodzi przez wierzchołek 
 Coś takiego ?
Coś takiego ? 


