Funkcja liniowa Oleńka: Dla jakiej wartości parametru m rozwiązaniem równania |x−1|=m+2 jest para liczby o przeciwnych znakach? Wiem jak rozwiązać graficznie. Ale algebraicznie nie do końca wiem co robić. Zaczęłam tak: x (−niesk do 1) −x+1=m+2 −x=m+1 x=−m−1 dla x<1 do niesk) x−1=m+2 x=m+3 x1*x2<0 (−m−1)(m+3)<0 m²+4m+3>0 delta=4 pierw z delty 2 m1=−3 m2=−1 m należą od(−niesk do −3) lub (−1 do niesk) I nie wiem czemu w odpowiedzich jest że tylko od (−1 do niesk). W sumie jak narysuję wykres też wychodzi tylko ten jeden przedział

Tadeusz: ... ciekawe rozwiązanie − Masz postać iloczynową ... z niej pierwiastki wprost. Ale Ty wymnażasz ... liczysz deltę potem pierwiastki. Tyle, że t ma się nijak do zadania −

john2: A gdyby tak dodać założenie m + 2 ≥ 0, co chyba jest nawet konieczne, bo wartość bezwzględna musi być nieujemna. Może wtedy wyjdzie.

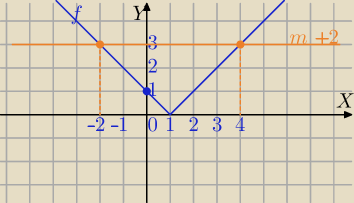Mila: Metoda graficzna . f(x)=|x−1| y=m+2 funkcja stała dla ustalonego m rozwiązaniem równania |x−1|=m+2 jest para liczb o przeciwnych znakach dla m+2>1⇔ m>−1