. aga: Wyznacz wszystkie wartości parametru k∈R dla których równanie (cosx+1/2)(sinx−k)=0 ma trzy różne rozwiązania w przedziale <0;2π> wiem ze x1=2π/3 x2=4π/3 i myslalam, ze k∈<−1;1> i ≠ od tych wartosci sinusa gdzie x1=2π/3 x2=4π/3, ale w odpwoiedziach jest inaczej i czemu wlasnie?

Tadeusz: a dlaczego k∊<−1;1> ?

aga: no to jak by to zrobic?

sushi_ gg6397228: najpierw podajesz rozwiazania dla pierwszego nawiasu−−> jakie to są i ile ich jest

aga: no napisalam przeciez ze x1=2π/3 x2=4π/3 i to sa rozwiazania z cosx=−1/2, ale mi chodzi o ten drugi nawias

sushi_ gg6397228: to kiedy sinus ma tylko jedno rozwiazanie na przedziałe <0; 2π> ?

aga: dla x ∈<π/2;3π/2>

sushi_ gg6397228: narysuj wykres sinusa i podaj odpowiedz; to nie LOTTO, że strzelamy

razor:

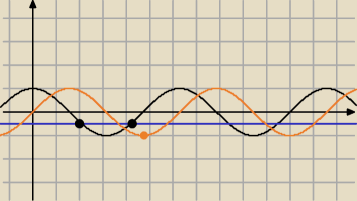
	1
czarne kropki to rozwiązania cosx = −
	2

teraz sinx = k musi mieć tylko jedno rozwiązanie w przedziale <0,2π> − pomarańczowa kropka

razor: znikła mi kropka jedna sinx = 1 też może być

aga: no to k=1 lub k=−1