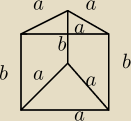
Optymalizacja jakubs: Dany jest graniastosłup prawidłowy trójkątny, którego suma długości krawędzi wynosi L. Oblicz, jakie muszą być długości krawędzi graniastosłupa, aby pole powierzchni bocznej było największe. 6a+3b=L Pb=3ab

	L−6a
b=
	3

	L−6a
Pb=3a*
	3

Pb=a(L−6a)

	L
Parabola skierowana ramionami ku dołowi, więc największe pole będzie dla a=
	12

Podstawiając dalej:

	L
6*		+3b=L
	12

L+6b=2L L=6b

	L
b=
	6

Jest ok?

Mila: Dobrze.

Saizou : ale jednak czegoś brakuje, co kosztuje 1 punkt na maturze (w najlepszym wypadku xd)

bezendu: Dziedzina

zawodus: Pokażcie mi, gdzie w arkuszu oceniania są odjęte punkty za dziedzinę?

jakubs: Czyli muszę dopisać, że a,b,L >0

Mila: D_f: L−6a>0 L>6a

	L
a<
	6

jakubs: Aa ok dziękuję Milu