geometria help: Na ramionach AC i BC trójkąta równoramiennego ABC wybrano punkty P i Q w ten sposób, że odcinek PQ jest równoległy do podstawy AB i styczny do okręgu wpisanego w trójkąt ABC . Wykaż, że pole trójkąta ABC jest równe:

|AB|2 * √|AB|*|PQ|
2* (|AB| − |PQ|)

Czy to robić z podobieństwa trójkątów CPQ i CAB, da mi to coś?

help: up

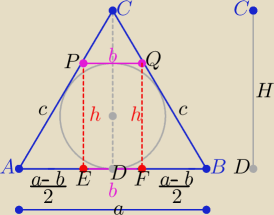Eta: Z warunku wpisania okręgu w trapez ABQP :

	a+b
a+b= 2c ⇒ c=
	2

	a−b
h(tr)=√c2−(		)2= .......... =√ab
	2

z podobieństwa trójkątów ABC i CPQ :

H		a		a√ab
	=		⇒ ................ H=
H−h		b		a−b

	1		a2√ab		|AB|2*√|AB|*|PQ|
P(ΔABC)=		*a*H= .............=		=
	2		2(a−b)		2(|AB|−|PQ|)

help: O dzięki, nie pomyślałam o tym trapezie i warunku wpisywalności, dzięki !

Eta: