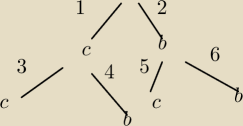
Prawdopodobienstwo jakubs: W urnie znajdują się kule białe i czarne w ilości 20 sztuk, w tym b kul białych. Losujemy jedną kulę z urny i zapisujemy wynik, po czym zwracamy kulę do urny. Czynność powtarzamy. Oblicz,dla jakiej wartości parametru b prawdopodobieństwo wylosowania kul w rożnych kolorach jest największe. Chciałbym rozwiązać to zadanie drzewkiem stochastycznym. c− wylosowanie kuli czarnej b− wylosowanie kuli białej

	20
1 −
	20+b

	b
2 −
	20+b

	20
3 −
	20+b

	b
4 −
	20+b

	20
5 −
	20+b

	b
6 −
	20+b

Póki co jest dobrze ?

Maslanek: Nie. Pośród 20 kul jest b białych. Czyli b − ilość białych 20−b − ilość czarnych

Maslanek: Sam tok rozumowania w porządku. Nie licząc tego, że nie czytasz poleceń ze zrozumieniem

jakubs: Dzięki, racja. Jak będę miał jeszcze pytania to się odezwę.

jakubs:

	20		b		20		b
P(A)=		*		+		*
	20−b		20−b		20−b		20−b

	40b
P(A)=
	(20−b)2

I co dalej ?

Maslanek: Bez sensu

20
	>1 Czy kiedykolwiek prawdopodobieństwo może być większe niż 1?
20−b

jakubs: No prawdopodobieństwo może być większe lub równe 1. Możesz napisać jak doszedłeś do tej nierówności ? Bo z 1 już rozumiem, ale ja liczyłem tak jak jest ze schematem przy drzewku.

jakubs: Co ja napisałem, prawdopodobieństwo może być mniejsze lub równe 1. Ale nadal nie mogę rozkminić

	20
jak doszedłeś do
	20−b

Maslanek: To Twój zapis Pomyliłeś licznik i mianownik

jakubs: Nie ogarniam już. Jak pomyliłem licznik i mianownik ?

jakubs: Jest ktoś w stanie mi to wytłumaczyć ?

Marcin: Wiesz ile jest tych kul.. 20. Więc przykładowo, prawdopodobieństwo wylosowania kuli białej (gdyby było ich np 11). to

	11		20
		. a nie jak w Twoim przypadku
	20		11

	b
Kul masz b, więc prawdopodobieństwo wylosowania tej kuli jest równe		.
	20

jakubs: Dzięki Marcin, źle zrozumiałem treść zadania