Problemy z ostrosłupem Jancio: Kąt między krawędzią boczną a podstawą ostrosłupa prawidłowego czworokątnego ma marę α, a kąt między jego krawędziami bocznymi ma miarę β. a) Wykaż żę cos β=sin²α b)Oblicz objętość tego ostrosłupa jeżeli β=60 stopni, a krawędź boczna ma długość 4

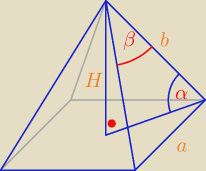
Godzio: Z twierdzenia cosinusów:

	2b2 − a2		1		a
a2 = b2 + b2 − 2b2cosβ ⇒ cosβ =		= 1 −		* (		)2
	2b2		2		b

	H
sinα =
	b

Z twierdzenia Pitagorasa:

	1		1
H2 + (		a√2)2 = b2 ⇒ H2 = b2 −		a2
	2		2

	1   b2 − a2   2		1
sin2α =		= 1 −		* a2
	b2		2

Zatem cosβ = sin²α

Godzio:

	a
Na samym końcu (		)2
	b

pigor: ..., lub a)z tw. cosinusów w ścianie bocznej (Δ równoramienny) i funkcji cosinus w Δ prostokątnym z kątem α w ostrosłupa :

	2b2−a2		12a√2
cosβ=		i cosα=		⇔
	2b2		b

⇔ cosβ= 1−¹₂(^a_b)² i ^a_b= √2cosα ⇔ cosβ= 1−¹₂(√2cosα)² ⇔ ⇔ cosβ= 1− cos²α ⇔ cosβ= sin²α c.n.w. −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− b) β=60^o i b=4 , to (*) V= ¹₃a²H= ? , gdzie z a) cos60^o= sin²α i α − ostry ⇒ sinα= ¹₂√2 ⇒ α=45^o , zatem H= bsinα= 4*¹₂√2= 2√2= ¹₂a√2 ⇒ a=b=4, więc z (*) V= ¹₃*4²*2√2 = ³²₃√2 − szukana objętość ostrosłupa .