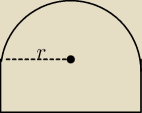
geometria help: Przedstawiona na rysunku figura składa się z półkola i prostokąta. Oblicz maksymalne pole tej figury , jeżeli jej obwód jest równy k.

Godzio: πr + a + 2b = k, ale a = 2r

	k − r(π + 2)
πr + 2r + 2b = k ⇒ b =
	2

	k − r(π + 2)
P= πr2 + ab = πr2 + 2r *		= πr2 − r2(π + 2) + 2kr
	2

= −2r² + 2kr = P(r) Wiemy, że wartość największa jest w wierzchołku:

	−2k		k
rw =		=
	−4		2

	k2		k		k2		k2
P(rw) = −2		+ 2k *		= −		+ k2 =
	4		2		2		2

minnie: a czy tam nie powinno być πr² − r²(π+2) + kr ?

Godzio: Owszem powinno być, dobrze że analizujesz, a nie przepisujesz

wiola: poza tym we wzorze na pole powinno być 1/2 πr², bo figura zawiera tylko połowę koła