30 kwi 16:28
Godzio:
A jaki jest Twój sposób?
30 kwi 16:29
bezendu:
Zniknął w czasoprzestrzeni

30 kwi 16:30
Hugo: Dwa równania rozpisujemy ze wzoru P(AuB)=P(A)+P(B)−P(AnB)
(AnB')
(A'n B)
P(AuB')=P(A)+P(B')−P(AnB')
P(A'uB)=P(A')+P(B)−P(A'nB) //dodajemy równania
Ω−P(AnB)= Ω +Ω −0,2 − 0,1
P(AnB)=−0,7 a ma być 0,7

30 kwi 16:31
Godzio:
Znaki są bez sens, P(Ω) = 1, nie można sobie tak pisać Ω
P(A U B') + P(A' U B) = 1 + 1 − 0.3 = 1.7
No i wytłumacz się z tego co dalej piszesz.
30 kwi 16:34
Hugo: WIDZE BŁĄD
P(AuB')+P(A'uB)=Ω+P(AnB) + P(A'nB')
ale to mi nie pomaga...
30 kwi 16:39
Godzio:
Nie pisz Ω, bo to nie jest poprawne!
Dla mnie ta równość dalej nie jest oczywista, wytłumacz się

30 kwi 16:41
Hugo: no bo rozpisuje według tego wzoru P(AuB)=P(A)+P(B)−P(AnB) i za ostatni wyraz podstawiam
(AnB')
(A'n B)
a potem chce dodać te dwa wzoru wierząc że mi sie uprości coś
30 kwi 16:42
Hugo: Otrzymuje dwa równania
P(AuB')=P(A)+P(B')−P(AnB')
P(A'uB)=P(A')+P(B)−P(A'nB)
30 kwi 16:42
Hugo: dodajemy
P(A'uB)+ P(AuB') =P(A')+P(B)−P(A'nB) + P(A)+P(B')−P(AnB')
30 kwi 16:42
Hugo: P(A'uB)+ P(AuB') =P(A')+ P(A)+P(B) +P(B')−P(AnB')−P(A'nB) // P(Ω) + P(Ω) =2
30 kwi 16:44
Godzio:
To akurat rozumiem, chodzi o to jak dodajesz P(A' U B) + P(A U B') (w kolejnym przejściu po
dodaniu równań już.
To mamy:
P(A U B') + P(A' U B) = 1.7
Co dalej?
30 kwi 16:44
Hugo: P(AnB') = 0,1
P(A'n B)=0,2
P(A'uB)+ P(AuB') =2 −0,3
30 kwi 16:45
Hugo: I trzeba rozpisać
P(A U B') + P(A' U B) = 1.7

daj sekundke
30 kwi 16:46
Godzio:
Ok, w początkowym rozwiązaniu dalej to jakoś wyliczałeś, co brało się nie wiadomo skąd

30 kwi 16:46
Hugo:

P(A U B') + P(A' U B) = 2− P(AuB)+P(AnB)
30 kwi 16:50
Hugo: a czy do tego momentu jest dobre

30 kwi 16:50
Godzio:
Tak, to było wszystko ok, pisałem to już 2 razy

30 kwi 16:52
Hugo: 2− P(AuB)+P(AnB) =1,7
− P(AuB)+P(AnB) =−0,7
utknąłem

30 kwi 16:54
Godzio:
A sory, myślałem, że to znów przepisałeś, właśnie tej równości (z rysunkiem) nie rozumiem. Daj
mi chwilę, żebym zobaczył czy tak na pewno jest, ale raczej nie.
30 kwi 16:56
Hugo: L= P(A U B') + P(A' U B) = P(B) + P(B') + P(A') + P(A) −( P(A'nB)+P(AnB') )
−( P(A'nB)+P(AnB') ) = −(1−P(AnB) )= −1 + P(AnB)

−1 + P(AnB) + 2 =1,7
P(AnB) =0,7

30 kwi 16:59
30 kwi 16:59
Hugo: PAtrz tylko na ostatni post:
P(A U B') + P(A' U B)=1,7
Do tego my tam wyzej doszli już i rozpisujemy tu lewą strone
P(A U B') + P(A' U B) ze wzoru.
i potem podstawiam do 1,7

30 kwi 17:01
Godzio:
P(A U B') = 1 − P(B \ A) = 1 − ( P(B) − P(A ∩ B) ) = 1 − P(B) + P(A ∩ B)
Analogicznie
P(A' U B) = 1 − P(A \ B) = 1 − (P(A) − P(A ∩ B) ) = 1 − P(A) + P(A ∩ B)
Jeżeli dodamy to mamy:
2 − P(A) − P(B) + 2P(A ∩ B) = 2 − P(A U B) + P(A ∩ B)
No dobra doszliśmy do tego co masz.
P(A U B) − P(A ∩ B) = 0.3
P(A∩B) = P(A U B) − 0.3 ≤ 1 − 0.3 = 0.7
No czyli musiałeś to dokończyć

30 kwi 17:02
Godzio:
Równości akurat nie ma

30 kwi 17:02
Hugo: Godzio ty student : P ?
30 kwi 17:02
Godzio:
Tak
30 kwi 17:03
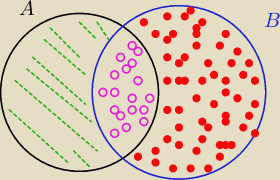 https://matematykaszkolna.pl/strona/3606.html
zad. 12
//wiem ze są odp ale chciałbym swoim sposobem i czemu jest zły
https://matematykaszkolna.pl/strona/3606.html
zad. 12
//wiem ze są odp ale chciałbym swoim sposobem i czemu jest zły P(AnB') = 0,1 (zielone paski)
P(A'n B)=0,2 (KROPKI)
wykaż że P(AnB)≤0,7
P(AnB') = 0,1 (zielone paski)
P(A'n B)=0,2 (KROPKI)
wykaż że P(AnB)≤0,7



 daj sekundke
daj sekundke

 P(A U B') + P(A' U B) = 2− P(AuB)+P(AnB)
P(A U B') + P(A' U B) = 2− P(AuB)+P(AnB)



 −1 + P(AnB) + 2 =1,7
P(AnB) =0,7
−1 + P(AnB) + 2 =1,7
P(AnB) =0,7 


















 WYSZŁO <3... chyba ! ale odp jest dobra
WYSZŁO <3... chyba ! ale odp jest dobra 


