analityczna mat: wyznacz wartość parametru m dla której odległość punktu P = (m², 3m −1) od prostej y=x+2 jest najmniejsza możliwa.

	|−m2 + 3m−3|
ta odległość wyszła mi d=
	√2

i co z tym dalej? rozbijać na m>0 i m<0 ?

J: f(m) = I −m² + 3m − 3 I ... i obliczasz f_min

Mila:

	|−m2+3m−3|
f(m)=		⇔
	√2

	|m2−3m+3|
f(m)=
	√2

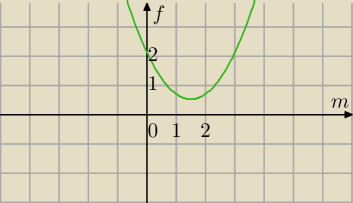
Δ=9−4*3<0⇔m²−3m+3 przyjmuje tylko wartości dodatnie⇔

	m2−3m+3
f(m)=
	√2

Najmniejsza wartość f(m) dla

	3
m=
	2