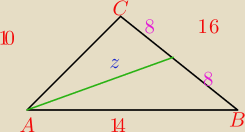
Planimetria Kamix: Cześć. Mam problem z pewnym zadaniem ; ) Proszę o pomoc ; DD W trójkącie o bokach 10;14;16 poprowadzono środkową do najdłuższego boku. Oblicz długość tej środkowej. Zastosuję tutaj układ równań, dwukrotnie wykorzystując twierdzenie cosinusów. z²=14²+8²−2*14*8*cosα z²=10²+8²*2*10*8cosα Mam układ dwóch niewiadomych i dwa równania, więc nie ma problemu z ich obliczeniem... z²=196+64−224cosα z²=260−224cosα Podstawiam z² do drugiego: 260−224cosα=100+64−80cosα −144cosα=−96

	2
cosα=
	3

Teraz podstawiam za cosα

	224*2
z2=260−
	3

z=U{2√84{√3}. Nie usuwałem już niewymierności z mianownika, bo wynik jest inny od tego z odpowiedzi. Proszę o pomoc..

bezendu: Na środkową w trójkącie jest gotowy wzór :http://pl.wikipedia.org/wiki/%C5%9Arodkowa_tr%C3%B3jk%C4%85ta

J: W obydwu równaniach użyłeś kąt α .... a to nie jest trójkąt równoramienny

Kamix: bezendu, ale czy na maturce mógłbym użyć tego wzoru bez żadnego wyprowadzania? Bo nie ma go w tablicach...

bezendu: Możesz, musisz napisać że korzystasz z tego

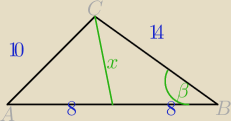
Kamix: Próbowałem zrobić to bez tego wzoru i też wynik mi się nie zgadza, co robię źle? Na początku wyznaczam cosβ 10²=16²+14²−2*16*14cosβ 100=256+194−448cosβ 448cosβ=350

	175
cosβ=
	224

No i teraz już prosto z twierdzenia cosinusów:

	175
x2=82+142−2*8*14*
	224

	175
x2=64+196−224*
	224

x²=85 x=√85 Wynik zły. Proszę o pomoc.

Piotr 10: 14²=196 a nie 194

Kamix: Dzięki Piotrek ; ) Jak zwykle całe zadanie sypie się przez jakąś błahostkę...

Mila: 15:32 − metoda dobra. Kamix, najpierw popatrz na długości boków, lepiej się liczy, gdy wybierzesz opcję obliczenia cosα. Sprawdź, może przyda się, a w każdym bądź razie utrwalisz wiadomości.

Kamix: Dziękuję Pani bardzo serdecznie ; ) Jutro z samego ranka wracam do tego zadanka i tak jak Pani radzi, dla utrwalenia policzę tego cosα z różnych boków ; P Teraz zajmuje się analityczną, nie chcę się odrywać, ale jutro liczę od nowa zadanko ; )