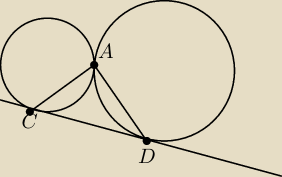
Dwa okręgi są styczne zewnętrzni w punkcie A. dawidek15: Dwa okręgi są styczne zewnętrznie w punkcie A. Poprowadzono prostą styczną do obu okręgów odpowiednio w punktach C i D. Oblicz miarę kąta CAD

dawidek15: od czego mam zacząć?

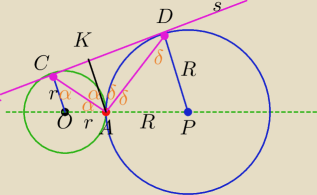
Mila: s − styczna do obu okręgów OC ⊥s AK ⊥s PD ⊥s OC||AK, AK||PD powstały trapezy i trójkaty równoramienne ΔADP, ΔCOA mają kąty przy podstawach równe. W trapezach masz kąty naprzemianległe wewnętrzne równe. 2α+2δ=180 α+δ=90 ∡CAD=90^o

dawidek15: jakoś to zrobiłem ale teraz jeszcze mam takie jedno równanie do rozwiązania a mianowicie x(x−1)(x+1)(x+2)=24 mi wyszło co prawda x=−2 i x=1 ale nie wiem czy to jest dobrze? mógłby ktoś to zrobić , ja zaraz przepiszę swoje rozwiązanie

zawodus: rzeczywiste rozwiązania to x=−3 lub x=2

5-latek: ma wyjsc x=−3 i x=2

dawidek15: x(x−1)(x+1)(x+2)=24 x(x²−1)(x+2)=24 x(x³+2x²−x−2)=24 x⁴+2x³−x²−2x−24=0 x³(x+2)−1(x²+2x+24)=0 (x+2)(x²+2x+24)(x³−1)=0 (x+2)(x²+2x+24)(x−1)(x²+x+1)=0 czy mój tok myślenia idzie w dobrą stronę ?

dawidek15: czyli już wyszły inne wyniki to jest na pewno źle może ktoś mi to rozpisać ?

zawodus: 5 linijka to bzdura totalna.

dawidek15: jak należy to rozpisać bo próbuję na różne sposoby i nadal mi nic nie wychodzi

zawodus: szukaj pierwiastków wymiernych

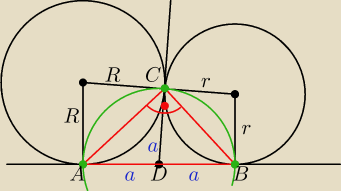
Bogdan: Zadanie dawidka można i tak ująć. Po wykazaniu, że |AD| = |DC| = |DA| = a, (a to długość promienia okręgu opisanego na trójkącie ABC) stwierdzamy: trójkąt wpisany w okrąg, którego jeden z boków jest średnicą tego okręgu, jest trójkątem prostokątnym.