Oblicz długość cięciwy
Paula:
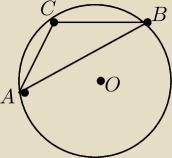
Promień okręgu jest równy 4
√2. Oblicz długość cięciwy AB.
Kąt ACB jest dany, to 105 stopni. Zastosowałam twierdzenie cosinusów dla trójkąta AOB gdzie kąt
AOB ma 150 stopni ale wynik nie zgadza się z odpowiedzią. Mógłby ktoś rozwiązać to żebym
zobaczyła gdzie robię błąd?
30 kwi 12:19
Hajtowy:
|AO| + |BO| = |AB|
(4√2)2 + (4√2)2 = |AB|
|AB| = √64 = 8
30 kwi 12:21
Hajtowy: Ale ja nie wiem − tak myślę... Niech ktoś mądrzejszy się wypowie
30 kwi 12:22
30 kwi 12:23
Paula: Jednak nigdzie nie było błędu, po prostu w odpowiedziach wynik był bardziej przekształcony.
Sposób jest dobry, wynik to
√32√3+64 lub prościej 4+4
√3. Może komuś się przyda
30 kwi 12:24
J: Najprawdopodobniej w obliczeniach, bo kąt 150o wyliczyłaś prawidłowo.
30 kwi 12:24