 Dany jest trójmian kwadratowy f o wspó?czynniku 2 przy najwy˝szej pot´dze x. Wierzcho?ek
paraboli b´dacej wykresem tego trójmianu ma wspó?rz´dne W = 5,− 10i. Wyznacz f (15).
f(x) = a(x−p)2 + q
W=(p,q) = (5,−10), a = 2
f(x) = 2(x−5)2 − 10
f(15) = 2(15−5)2 − 10 = 2(10)2 − 10 = 2*100 − 10 = 200 − 10 = 190
2)
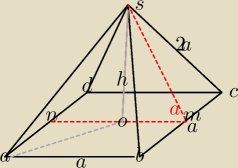
Dany jest ostros?up prawid?owy czworokatny o kraw´dzi bocznej dwa razy wi´kszej od kraw´dzi
podstawy.
a) Wyznacz cosinus kata nachylenia Eciany bocznej do p?aszczyzny podstawy ostros?upa.
b) Wyznacz d?ugoEç kraw´dzi ostros?upa, tak aby pole jego powierzchni bocznej wynosi?o 36
pierwiastek z 15
Dany jest trójmian kwadratowy f o wspó?czynniku 2 przy najwy˝szej pot´dze x. Wierzcho?ek
paraboli b´dacej wykresem tego trójmianu ma wspó?rz´dne W = 5,− 10i. Wyznacz f (15).
f(x) = a(x−p)2 + q
W=(p,q) = (5,−10), a = 2
f(x) = 2(x−5)2 − 10
f(15) = 2(15−5)2 − 10 = 2(10)2 − 10 = 2*100 − 10 = 200 − 10 = 190
2)
Dany jest ostros?up prawid?owy czworokatny o kraw´dzi bocznej dwa razy wi´kszej od kraw´dzi
podstawy.
a) Wyznacz cosinus kata nachylenia Eciany bocznej do p?aszczyzny podstawy ostros?upa.
b) Wyznacz d?ugoEç kraw´dzi ostros?upa, tak aby pole jego powierzchni bocznej wynosi?o 36
pierwiastek z 15
| OM | ||
cos α = | ||
| SM |
| a | ||
lOMl = | ||
| 2 |
| a | ||
(2a)2 = ( | )2 + lSMl2 | |
| 2 |
| a2 | ||
4a2 = | + SM2 | |
| 4 |
| a2 | 15 | √15a | ||||
4a2 − | = lSMl2 => SM2 = | *a2 => lSMl = | ||||
| 4 | 4 | 2 |
| 1 | √15 | ||||||||||
cos a = | = | = | ||||||||||
| √15 | 15 |
| 1 | √15a | |||
b) Pb = 4 * | * a * lSMl = 2a* | = √15*a2 | ||
| 2 | 2 |
 ?
to co pod pierwiastek musi byc nieujemne ( ≥ 0 )
x2 ≥ 0 −x2 ≥ 0
x ∊ R x = 0 , wiec Df = {0}
?
to co pod pierwiastek musi byc nieujemne ( ≥ 0 )
x2 ≥ 0 −x2 ≥ 0
x ∊ R x = 0 , wiec Df = {0}