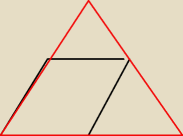
Trójkąt i wpisany w niego romb mają wspólny kąt Johny: Trójkąt i wpisany w niego romb mają wspólny kąt. Stosunek długości boków zawierajacych ten kąt wynosi k. Wyznacz stosunek pola rombu do pola trójkąta To będzie taki rysunek? nie rozumiem o co chodzi z tym stosunkiem

Tadeusz: ... to jest dokładna treść zadania?

Bogdan: Te informacje wystarczą do rozwiązania zadania

Domel: A co mi tam − raz dla odprężenia może coś rozwalę

a
	= k => a = k*b
b

H
	= sinα => H = b*sinα
b

	1		1
PΔ =		a*H =		*k*b*b*sinα
	2		2

	1
PΔ =		*k*b2*sinα
	2

Ponieważ w trójkąt jest wpisany romb to: x = y

x
	= k => x = k*(b−y) = k*(b−x)
b−y

x = k*b − k*x => x*(k+1) = k*b

	k*b
x =
	k+1

h		h		k*b
	=		= sinα => h = x*sinα =		*sinα
y		x		k+1

	1		1		k*b		k*b
P[] =		*x*h =		*		*		*sinα
	2		2		k+1		k+1

	1		k2*b2
P[] =		*		*sinα
	2		(k+1)2

P[]		k2*b2   *sinα 2*(k+1)2		k
	=		=
PΔ		1   *k*b2*sinα 2		(k+1)2

Domel: A co mi tam − raz dla odprężenia może coś rozwalę

a
	= k => a = k*b
b

H
	= sinα => H = b*sinα
b

	1		1
PΔ =		a*H =		*k*b*b*sinα
	2		2

	1
PΔ =		*k*b2*sinα
	2

Ponieważ w trójkąt jest wpisany romb to: x = y

x
	= k => x = k*(b−y) = k*(b−x)
b−y

x = k*b − k*x => x*(k+1) = k*b

	k*b
x =
	k+1

h		h		k*b
	=		= sinα => h = x*sinα =		*sinα
y		x		k+1

	1		1		k*b		k*b
P[] =		*x*h =		*		*		*sinα
	2		2		k+1		k+1

	1		k2*b2
P[] =		*		*sinα
	2		(k+1)2

P[]		k2*b2   *sinα 2*(k+1)2		k
	=		=
PΔ		1   *k*b2*sinα 2		(k+1)2

Domel: Sorki − coś mi komp dubluje

Bogdan: Proponuję znaleźć prostsze i krótsze rozwiązanie

pigor: ..., a ja widzę to tak: niech P_r , P − pole rombu i ΔABC odpowiednio, a P₁,P₂ − pola trójkątów podobnych (kkk) do ΔABC w skali k, odciętych przez romb o którym mowa w zadaniu, wtedy

Pr		P−P1−P2		P1
	=		= 1− 2		= 1−2k2 − szukany stosunek.
P		P		P

przy czym 0<1−2k²<1 ⇔ k²<¹₂ i k>0 ⇔ 0< k <¹₂√2; −−−−−−−−−−−−−−−−−−−−−−−−−−−−−− kurcze czy coś robię nie tak w tym... prostym rozwiązaniu ...

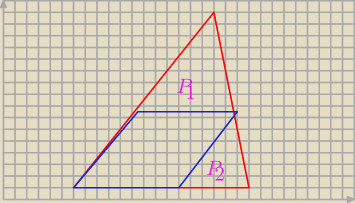Domel: Wg mnie − trójkąty P₁ i P₂ są podobne ale nie takie same − coś mi pigor twój wynik nie pasi

pigor: hmm..., nie mówię o równości pól P₁ i P₂, tylko o równości

	P1		P2
stosunków pól		=		3−ech trójkątów parami podobnych .
	P		P

−−−−−−−−−−−−−−−−−−−−−−−−−−−− może ktoś jeszcze się wypowie

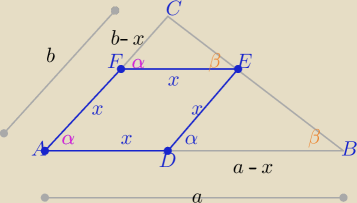Eta: Trójkąty ABC i DBE i EFC są podobne z cechy (kkk)

	a
z treści zad.		=k ⇒ a=k*b
	b

	x		a		x		kb
to		=		⇒		=k ⇒ x=
	b−x		b		b−x		k+1

	k2b2
P(rombu)= x2*sinα =		*sinα
	(k+1)2

	ab		kb2
P(ABC)=		*sinα =		*sinα
	2		2

P(robu)		2k
	=
P(ABC)		(k+1)2

Domel:

	1
Eta − podporo i filarze drużyny − nie wiem skąd mi się wzięła		w polu rombu.
	2

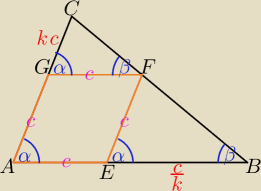Bogdan: Bez skrótów:

|AC|
	= k
|AB|

Trójkąty ABC, EBF, GFC są podobne.

|GC|		|EF|		c
	= k ⇒ |GC| = kc,		= k ⇒ |EB| =
|GF|		|EB|		k

pole rombu		c2*sinα
	=		=
pole trójkąta ABC		1   c   *(c + kc)(c + )*sinα 2   k

	2c2sinα		2		k
=		=		*		=
	1   c2*sinα(1 + k)(1 + )   k		1   1 + + k + 1   k		k

	2k		2k
=		=
	2k + 1 + k2		(k + 1)2