planimetria razor: Jak mam takie śmieszne zadanie W trójkącie ABC dane są |AB| = 8, |∡ABC| = 20 st., |∡CAB| = 30 st. Oblicz długości boków trójkąta oraz długość promienia okręgu wpisanego w trójkąt. to da się to rozwiązać bez używania sin130/20? Czy wtedy mam to przybliżyć z karty wzorów czy zostawić tak jak jest?

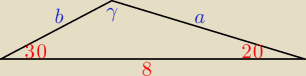
Bogdan: Pomijam znak ^o przy mierze kąta, r − długość promienia okręgu wpisanego, γ = 130, sinγ = sin(180 − 50) = sin50

	a		8
Z twierdzenia sinusów:		=		⇒ a = ...
	sin30		sin50

Podobnie obliczamy wartość b

	1		1
Pole trójkąta P =		*8*sin30, Obwód L = a + b + 8, P =		L*r ⇒ r = ...
	2		2

Trzeba odczytać wartości potrzebnych funkcji trygonometrycznych z tablic

Bogdan:

	1
P=		*8*b*sin30.
	2

razor: Bogdan ja wiem jak to zadanie zrobić moje pytanie brzmiało czy jak coś takiego trafi się na maturze to czy powinienem przybliżać sin z tablic, zostawić tak jak jest, czy może próbować innej metody?

Bogdan: Odpowiedziałem, że trzeba odczytać wartości z tablic. Dodam − wybieramy wartości najbliższe

zombi: Ah ta matura PWN.