geometria maja: na boku BC równobocznego trójkąta ABC wybrano taki punkt D, że stosunek pola trójkąta ADB do pola trójkąta ADC wynosi 1:2. Wyznacz tangens kąta DAB.

Eta:

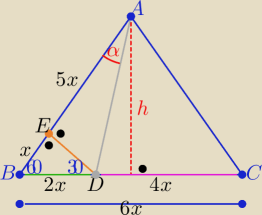
P(ADB)		1
	=		−− trójkąty mają wspólną wysokość h
P(ADC)		2

to |BD|=2x , |DC|=4x , x>0 Z trójkąta DEB "ekierki" 60^o,30^o,90^o |BE|=x , |AE|=5x , |ED|=x√3

	|ED|		√3
tgα=		=
	|AE|		5

pigor: ..., lub z warunków zadania i danego stosunku pól : P_ADB : P_ΔACD= ¹₂ = sinα : sin(60^o−α} ⇔ 2sinα= sin(60^o−α) ⇔ ⇔ 2sinα= sin60^ocosα−sinαcos60^o ⇔ 2sinα= ¹₂√3cosα−¹₂sinα /*2 ⇔ ⇔ 4sinα+sinα= √3cosα /:cosα ⇔ 5tgα= √3 ⇔ tgα= ¹₅√3 . ...

Eta:

pigor: ..., czy coś mam wyjaśnić ....

Eta:

Eta: Dla mnie? wszystko jasne .... ciekawe co odpowie maja

Mila: Maja z obrazu Goi, która? Ubrana?

pigor: ..., no właśnie to ... niedomówienia w moich (nie)gotowcach . ...