trygonometria-równiania, nierówności Natalia: Chciałabym wiedzieć czy dobrze rozwiązałam zadania, jeśli ktoś mógłby podać odpowiedzi to byłabym wdzięczna 1.Rozwiąż nierówność: a. tgx≥−1 b. 2cosx−1≤0 2. Rozwiąż równanie a. sin(x−^π₆)=1 b. 2cos²+sinx−2=0 c. sin2x+sin6x=0 3. Narysuj wykres funkcji y=|sin2x|−1. Podaj zbiór wartości oraz okres zasadniczy tej funkcji. Wymień miejsca zerowe tej funkcji należące do przedziału <−π,π>

Mila: Wpisz w wolfram i uzyskasz wyniki.

Natalia: coś mi się nie sprawdza niestety na tej stronie

Mila: 1) a) tgx≥−1 Zał.

	π
cosx≠0⇔x≠		+kπ, k∊C
	2

	π
tgx jest funkcja rosnącą , tgx=−1⇔x=−
	4

	−π		π
x≥		+kπ i x<		+kπ to można zapisać tak:
	4		2

−π		π
	+kπ ≤x<		+kπ, k∊C
4		2

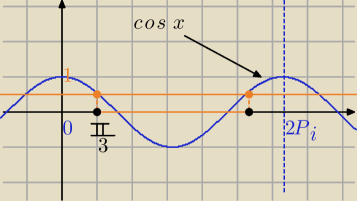Mila: 1) b) 2cosx−1≤0⇔

	1		1		π		π
cosx≤		[cosx=		⇔x=		lub x=2π−		]
	2		2		3		3

odczytujesz z wykresu dla jakich argumentów wykres g(x)=cosx leży poniżej prostej y=2

π		5π
	+2kπ≤x≤		+2kπ
3		3