stereometria Robak: Cześć! Macie jakieś fajne zadanka ze stereometrii? Jak tak robię poprzednie matury to raz mi wychodzą zadania, a raz w ogóle nie wiem z której strony mam się za to zabrać. Przerobiłem z łatwością zadania wprowadzające z kiełbasy, ale już te maturalne sprawiają mi trudność. Może macie jakieś fajne? Np. ze zastosowaniem odwrotności talesa, podobieństwem itd.?

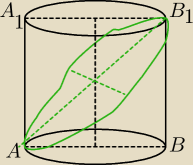
dero2005: Na podstawach walca przeprowadzono dwie rwnoległe średnice AB i A₁B₁. Przez końce A i B₁ tych średnic poprowadzono plaszczyznę styczną do okręgów będących brzegami podstaw. Powstały w ten sposób przekrój walca jest elipsą, której pole jest 4 razy większe od pola podstawy. Oblicz pole całkowitej powierzchni walca wiedząc, że duża oś elipsy przekroju jest równa 16 cm.

dero2005: Trapez równoramienny o ramieniu b i kącie ostrym α obraca się dookola wiekszej podstawy. Znaleźć objetość i pole powierzchni powstałej bryły wiedząc, że przekątna trapezu jest prostopadła do ramienia.

dero2005: Dany jest stożek o objętości V, którego tworząca jest nachylona do płaszczyzny podstawy pod kątem α. W jakiej odległości od wierzchołka stożka należy przeprowadzić płaszczyznę prostopadłą do osi stożka, żeby płaszczyzna ta podzieliła na połowy pole powierzchni bocznej stożka.

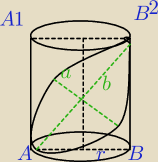
Robak: Z elipsą się pierwszy raz spotykam, ale znalazłem wzór na pole więc zaczynamy. Pcw=2*π*r²+2*π*r*H Pe=pole elipsy=4Pp π*a*b=4*π*r² |AB1|=16 Mogę jakąś małą podpowiedź czy dobrze robię?

Robak: Teraz chciałem z tych wzorów wyznaczyć H Mam, że b=8 kurczę.. nie wiem co dalej.

dero2005: a = r

Robak: (2r²)²+H²=16² H²=256−4r⁴ H=√256−4r⁴ H=16−2r² Pe=π*r*8 Pcw=2*π*r*8 + 2*π*r*16−2r² 2r(24π−r) r=0 r=24π Dobrze rozumuje czy nadal źle?

dero2005: Twój post 23:28 πab = 4πr² a = r πrb = 4πr² b = 8 → post 23:28 b = 4r

	b
r =		=
	4

dalej Pitagoras liczysz h

Robak: h wychodzi 0?

Robak: skoro b=8 to r=2 AB=2R=4 H²+4²=16 H²=16−16 ?

euler: Takie zadanko Dany jest stożek ścięty, którego wysokość jest średnią geometryczną średnic podstaw. Wykaż, że w ten stożek można wpisać kulę.

Robak: Dzięki zaraz się za to zabiorę tylko pierw ogarnę to 1 Próbuje znaleźć gdzie mam błąd

Robak: H=4√15 r=2 czyli Pcw=16√15π+8π

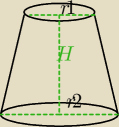
Robak: H=√2r₁*2r₂ Czyli muszę wykazać, że H jest prostopadłe do podstawy?

Robak: Przydałby się ktoś kto by ze mną je robił albo jakieś wskazówki No cóż pozostaje czekać, idę robić prawdopodobieństwo

Robak: Cześć odświeżam, mógłby ktoś spojrzeć?

zawodus: H jest zawsze prostopadłe do podstawy. To wynika z tego, czym jest H.

Robak: No to się później domyśliłem, ale jak sie za to zadanie zabrać?

zawodus: Do wykazania jest, że w przekrój osiowy (trapez równoramienny) można wpisać okrąg.