Prawdopodobieństwo Pati: Niech A i B będą zdarzeniami losowymi zawartymi w Ω. Wiadomo, że P(A∩B')=3/10 , P(A∩B)= 1/5 , P(AUB)= 9/10. Oblicz P(A) i P(B). W odpowiedziach jest P(A)=1/2 i P(B)= 3/5. Mi wyszło P(A)= 2/5, i P(B)= 7/10 Mógłby ktoś wytłumaczyć dlaczego P(A)=1/2 i P(B)= 3/5? Byłabym wdzięczna.

Pati: stfu. wyszło mi P(B)= 5/10

muflon: już tłumaczę

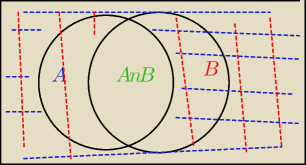
muflon: niebieskie kreski to A' czerwone kreski to B' P(A∩B')=P(A−B)=P(A)−P(AnB) P(AnB)=P(A)+P(B)−P(AuB) Z pierwszego policz P(A) Z drugiego P(B)

muflon: * mały błąd w rysunku! czerwona kreska nie powinna być w obrębie zbioru B

Pati: P(A∩B')=P(A−B)=P(A)−P(AnB) Hmm wyszło tak jak powinno być ale nadal nie rozumiem jednej rzeczy. Skoro AUB = 9/10 to P(A'nB')= 1/10 Dlaczego nie uwzględniamy tej części i nie ma P(AnB')= P(A) − P(AnB)+ P(A'nB') ?

Pati: dobra, wiem. Przecież to iloraz a nie suma. Wszystko jasne.