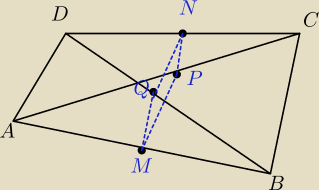
Dowód muflon: Niech ABCD bd dowolnym wypukłym czworokątem ( ale nie równoległobokiem). M i N to środki przeciwległych boków, a PQ to środki przekątnych. Pokaż, że te pkt tworzo równoległobok.

Pati: Jest takie twierdzenie. 'Jeżeli w dowolnym trójkącie połączymy środki dowolnych dwóch boków, to powstały odcinek jest równoległy do trzeciego boku i jego długość jest równa połowie długości boku trzeciego' Zauważ że przykładowo odcinki QN i PM są równoległe do tego samego boku− CB. Analogicznie QM i NP są równoległe do boku DA. Widać już wnioski?

muflon: O jak miło, ja Ci pomagam w prawdopodobieństwie, a Ty mi w planimetrii

muflon: To twierdzenie to w sumie Tales