Proste zadania z wektorow do wytłumaczenia tohino: Mam dla was pare zagadek matematycznych bardzo bym prosil zeby mi ktos wytlumaczyl bo nie rozumiem tych zadan: 1)Dane są punkty: A(1,4) B(6,−2) C (3,2) Wyznacz: AB, |AB|, u=AB+CA i znajdz D, aby AB=2CD 2) Dane są AC = [12,3] BC = [9,9] A (−5,3). Wyznacz równanie prostej zawierajacej wysokość opuszczona z punktu A. 3) Znajdź obraz obraz okregu x²−4x+y²−4y=0 w jednoukladnosci o srodku S(−4,−4) i skali k=2 4) Wyznacz m, dla ktorego 3u+4v−mw=0 jeśli u=[4,2] v=[−6,9] w=[−3,3/2]. Są to proste zadana ale prosze was o wytlumaczenie tego jak dla blondyki bo tego nie rozumiem. Pozdrawiam

tohino: Prosze was o pomoc

tohino:

tohino: Prosze

tohino:

daras: już po dobranocce wiec idź spać

PW: 4) Mnożenie wektorów przez liczbę wykonuje się w ten sposób, że mnoży się przez tę liczbę każdą współrzędną: 3u^→ = 3[4, 2] = [12, 6] 4v^→ = 4[−6, 9] = [−24, 36]

	3		3m
mw→ = m[−3,		] = [−3m,		].
	2		2

Dodawanie (odejmowanie) wektorów wykonuje się w ten sposób, że dodaje się (odejmuje) odpowiednie współrzędne − wynik jest wektorem, którego pierwsza współrzędna jest sumą (różnicą) pierwszych współrzędnych, a druga współrzędna jest ...:

	3m
3u→+4v→ − mw→ = [12, 6] + [−24, 36] − [−3m,		] =
	2

	3m		3m
= [12+ (−24) −(−3m), 6+36−		] = [−12+3m, 42−		].
	2		2

Zgodnie z treścią zadania wektor ten ma być równy wektorowi zerowemu 0^→ = [0, 0]. Równość wektorów oznacza równość ih odpowiednich współrzędnych, to znaczy

	3m		3m
[−12+3m, 42−		] = [0, 0] ⇔ −12+3m = 0 ∧ 42−		= 0 ⇔ m = 4 ∧ m = 28
	2		2

Odpowiedź: Nie istnieje liczba m spełniająca warunki zadania (chyba że pomyliłem się w rachunkach, trzeba to sprawdzić). Sprawdźmy tak: 3u^→+4v^→ = [12, 6] + [−24, 36] = [−12, 42] − nie jest to wektor równoległy

	3m
do wektora mw→ = [−3m,		] (sprawdź dlaczego), a więc równość podana w zadaniu nie
	2

może mieć miejsca dla żadnego m (jeżeli wektory są niezerowe, to mogą dać sumę zerową tylko wtedy, gdy są równoległe).

tohino: Dziękuję ci bardzo Jak sprawdziłem to pomyliłeś sie w wyniku jak sprawdziłem twoja metoda to m=12 ∧ m = 28 A mógłby ktoś jeszcze wytłumaczyć zadanie 2 lub/i 3

tohino: A mógłby ktoś jeszcze wytłumaczyć zadanie 2 lub/i 3

zośka: 1) wektor AB wyznaczamy tak, że od współrzędnych końca odejmujemy współrzędne początku, czyli wektor AB=[6−1, −2−4]=[5,−6] wektor CA=[3−1,2−4]=[2,−2] długość wektora |AB|=√5²+(−6)²=√61 u=AB+CA=[5,−6]+[2,−2]=[5+2, −6+(−2)]=[7,−8] Niech D=(x,y) CD=[x−3, y−2] 2CD=[2(x−3), 2(y−2)] 2CD=AB czyli [2(x−3), 2(y−2)]=[5,−6] 2(x−3)=5 i 2(y−2)=−6

	11
x=		i y =−1
	2

Janek191: 2) → AC = [ 12; 3 ] → BC = [ 9 ; 9] A = ( − 5; 3) Niech C = ( x₁; y₁), więc → AC = [ x₁ − (−5); y₁ − 3] = [ 12; 3] x₁ + 5 = 12 i y₁ − 3 = 3 x₁ = 12 − 5 = 7 i y₁ = 3 + 3 = 6 czyli C = ( 7 ; 6) ============= Niech B = ( x₂; y₂), więc → BC = [ 7 − x₂; 6 − y₂ ] = [ 9 ; 9 ] 7 − x₂ = 9 i 6 − y₂ = 9 x₂ = 7 − 9 = − 2 i y₂ = 6 − 9 = − 3 czyli B = ( − 2 ; − 3) =============== Równanie prostej BC : y = a x + b − 3 = − 2a + b 6 = 7 a + b −−−−−−−−−−−−−−− odejmujemy stronami 6 − ( −3) = 7a − ( −2a) 9 = 9a a = 1 −−− b = 6 − 7a = 6 − 7*1 = − 1 −−−−−−−−−−−−− y = x − 1 ====== Prosta zawierająca wysokość poprowadzoną z punktu A jest prostopadła do pr AC, wiec 1*a₂ = − 1 ⇒ a₂ = − 1 y = − x + b₂ oraz A = (− 5; 3), zatem 3 = − (−5) + b₂ 3 = 5 + b₂ b₂ = − 2 y = − x − 2 =========

zośka: zadanie2) AC=[x_C−x_A, y_C−y_A] AC=[12,3] zatem:x_C−x_A=12 i y_C−y_A=3 x_C−(−5)=12 i y_C−3=3 x_C=7 i y_C=6 czyli C=(7,6) Podobnie znajdujemy współrzędne B: BC=[x_C−x_B, y_C−y_B] BC=[9,9] 7−x_B=9 i 6−y_B=9 x_B=−2 i y_B=−3 B=(−2,−3) Znajdujemy teraz równanie prostej zawierającej bok BC: Zaczynamy od postaci ogólnei y=ax+b i podstawiamy raz współrzędne punktu B a raz współrzędne punktu C: −3=a*(−2)+b 6=a*7+b i rozwiązujemy ten układ równań; z pierwszego mamy :b=2a−3 wstawiamy to do drugiego: 6=7a+2a−3 9a=9 a=1 b=2*1−3=−1 prosta BC: y=x−1 Prosta zawierająca wysokość spuszczoną z wierzchołka A na bok BC jest do niej prostopadła, a więc ma równanie: y=−x+b' i przechodzi przez A, czyli: 3=−(−5)+b' (podstawiłam współrzędne A) b'=−2 Szukana prosta zawierająca wysokość spuszczoną z wierzchołka A ma postać zatem: y=−x−2

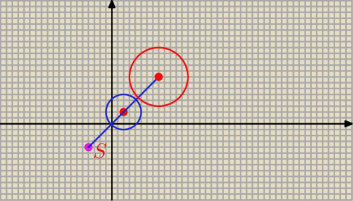
Janek191: 3) x² − 4 x + y² − 4 y = 0 ( x − 2)² − 4 + ( y − 2)² − 4 = 0 ( x − 2)² + ( y − 2)² = 8 ⇒ r² = 8 ⇒ r = 2√2 zatem środek okręgu O = ( 2; 2) i r = 2√2 oraz S = ( − 4; − 4) i k = 2 Niech O' = ( x' ; y' ) więc → → SO' = 2 SO [ x' − (−4); y' − (−4)] = 2*[ 2 − (−4); 2 − (−4) ] [ x' + 4; y' + 4 ] = 2*[ 6 ; 6 ] = [ 12; 12 ] x' + 4 = 12 i y' + 4 = 12 x' = 8 i y' = 8 czyli O' = ( 8 ; 8 ) oraz r' = 2*r = 2 *2√2 = 4 √2 ⇒ r'² = ( 4√2)² = 32 Odp. ( x − 8)² + ( y − 8)² = 32 =======================