cos2x+sin2x Kama: cos2x+sin2x. Jak uzależnić takie wyrazenie od jednej funkcji?

Mila:

	π
cos(2x)=sin(		−2x)
	2

Kama: Jednak tak sobie nie poradzę.

	1
Mam takie zdanie: Wyznacz dziedzinę funkcji f(x)=log(π−x2)+		Nie moge rozbić
	cos2x+sin2x

mianownika. Prosze o pomoc.

Nieuchwytny: π−x²>0 ⋀ cos2x+sin2x≠0

Kama: xE(−pi,pi) a drugiego nie wiem jak rozwiązać

ICSP:

	π
sin2x + cos2x = √2(sin(2x +		))
	4

Kama: Jestem za głupia na matematykę Mogę prosić kogoś o rozwiązanie zadnia?

ICSP: tak łatwo to nie ma

Nieuchwytny: π−x²>0 (π−x)(π+x)>0 x∊(−π,π) cos²x+sin²x≠0 ⇔ tg2x≠−1

	3π		kπ
x≠		+
	8		2

	−5π		3π
Dziedzina funkcji: (−π,π)\{		,		}
	8		8

Nieuchwytny: k∊C

Kama: Skąd wziął się tg2x≠−1 A wynik jest inny niż mam w odpowiedzi.

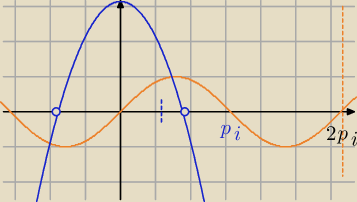
Mila: f(x)=π−x² π−x²>0⇔ Dziedzina x∊(−√π,√π) cos(2x)+sin(2x)≠0⇔

	π
sin(		−2x)+sin(2x)≠0
	2

	π   2		π   −4x 2
2sin (		*cos		≠0⇔
	2		2

	π
cos(		−2x)≠0
	4

	π		π
2x−		≠		+kπ⇔
	4		2

	3		kπ
x≠		π+
	8		2

dla k=0

	3
x=		π<√π wyłączymy z Df
	8

k=1

	3		π		7
x=		π+		=		π>√π, nie interesuje nas
	8		2		8

k=−1

	−1
x=		π wyłączymy z Df
	8

	π		−π		3		3
(−√π,−		)∪(		,		π)∪(		π,√π)
	8		8		8		8

pigor: ... , cos2x+sin2x ≠ 0 / : cos2x≠ 0 ⇔ 1+tg2x≠ 0 i cos2x≠ 0 ⇔ ⇔ tg2x≠−1 i cos2x≠0 ⇔ 2x≠−¹₄π+kπ i 2x≠¹₂π+kπ i 2x≠−¹₂+kπ ⇔ ⇔ x≠−¹₈π+¹₂kπ i x≠¹₄π+¹₂kπ i x≠−¹₄π+¹₂kπ ⇔ ⇔ x≠ −¹₈π(1−4k) i x≠ ¹₄π(1+2k) i x≠−¹₄π(1−2k) i k∊C.