Planimetria - okręgi Proximite: Witam Prosiłbym o rozwiązanie/pomoc przy tym zadaniu: Dany jest okrąg o (O,6). Oblicz długość cięciwy okręgu wyznaczonej przez tą sieczną okręgu, której odległość od punktu O jest równy 3√2.

PW: Widać trójkąt równoramienny (o ramionach długości r = 6) i wysokości 3√2. Mamy policzyć podstawę tego trójkąta. W czym problem, Pitagorasie?

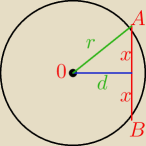
Janek191: r = 6 d = 3√2 więc x² = r² − d² = 6² − ( 3√2)² = 36 − 9*2 = 18 = 9*2 x = √9*2 = 3√2 Długość cięciwy I AB I = 2 *x = 2*3√2 = 6√2 =========================