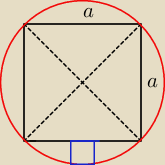
moglby ktos pomoc o co chodzi: Na kwadracie o boku długości a opisano koło. W jeden z otrzymanych odcinków kołowych wpisano kwadrat tak, że jeden z jego boków zawarty jest w boku kwadratu wyjściowego, a dwa pozostałe wierzchołki należą do okręgu, który jest brzegiem koła. Oblicz długość "nowego" kwadratu."

Janek191:

J:

	1
Długość boku nowego kwadratu wynosi: r −		a , gdzie r − promień okręgu, równy połowie
	2

przekatnej duzego kwadratu

J: Wycofuję wpis ... to nieprawda.

PW: Ale rozwiązanie jest chyba prościutkie. Połączyć środek dużego kwadratu z lewym dolnym wierzchołkiem małego − mamy odcinek o długości r. Połączyć środek dużego kwadratu i środek

	a
dolnego boku kwadratu małego − mamy odcinek o długości		+x. Twierdzenie Pitagorasa
	2

powinno da odpowiedź.