Plani <3
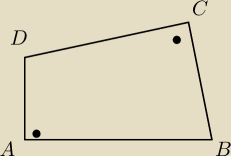
jakubs: Dany jest czworokąt ABCD, w którym długości boków wynoszą |AB|=14, |CD|=30, |AD|=48 oraz katy
DAB i BCD są proste. Oblicz pole tego czworokąta oraz długości jego przekątnych.
Można prosić o rysunek, bo nie potrafię go zrobić

28 kwi 12:07
Piotr 10:
28 kwi 12:08
jakubs: Dzięki

28 kwi 12:11
jakubs:
Czas na ostrosłup

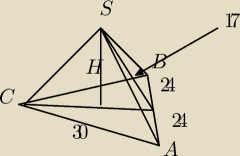
Dany jest ostrosłup ABCD, w którym podstawa jest trójkąt równoramienny ABC i |AB|=48,
|BC|=|AC|=30, a spodek wysokosci ostrosłupa nalezy do jego podstawy. Każda wysokość ściany
bocznej poprowadzona z wierzchołka S ma długość 17. Oblicz objętość tego ostrosłupa.
Rysunek ok ?
28 kwi 13:08
jakubs: ?
28 kwi 13:20
pigor: ... , może być, tylko jeszcze musisz zauważyć (stwierdzić),
że spodek wysokości H jest środkiem okręgu wpisanego w podstawę
ABC, a wtedy rozwiązanie stanie się...

proste.
28 kwi 13:31
jakubs: Ja to zacząłem robić tak, że wyznaczyłem krawędź boczną =
√865, wysokość podstawy =18
I zrobiłem układ równań, H
2+x
2=17
2 i H
2+(18−x)
2=865
Ale z tego x=7 więc coś nie tak

28 kwi 13:36
jakubs: x=−7*
28 kwi 13:36
pigor: .., a po co ci krawędź boczna
do szukanej objętości V=
13 P
ABC*H=

28 kwi 13:47
pigor: ..., H
2=17
2−r
2, gdzie r=
Sp
S − pole podstawy, p − połowa obwodu podstawy

28 kwi 13:50
jakubs: No tak próbowałem...
Z tym okręgiem wpisanym to nie wiem jak to ruszyć dalej.
28 kwi 13:51
jakubs: P=
√54*24*24*6
P=432
H
2=289−64
H=15
V=2160
Dzięki pigor
Po co ja się porywałem na to rozszerzenie ........
28 kwi 14:00
pigor: ... , właśnie po to, jednak wiesz dużo, a nie od razu Kraków
zbudowano ; trzymaj się, efekty przyjdą ...

same, ale ...z czasem i tyle . ...

28 kwi 15:37
jakubs: Czarno to widzę

Oblicz, ile jest liczb naturalnych siedmiocyfrowych, w zapisie których występuje dokładnie trzy
razy cyfra 7, dokładnie dwa razy cyfra 0 oraz dokładnie raz występuje cyfra 1.
| | | |
0 mogę wybrać na | sposobów |
| | |
| | | |
7 mogę wybrać na | sposobów |
| | |
1 mogę wybrać na 2 sposoby
Zostały mi cyfry 2,3,4,5,6,8,9
Czyli je mogę wybrać na 7 sposobów
Ostatecznie 15*10*2*7=2100
Dobrze?
28 kwi 15:58
jakubs:

I znowu planimetria <3
W trójkącie ABC dane sa długości boków |AC|=20 i |BC|=20.Na boku AB leży punkt D, taki ze |AD|
: |DB=11:10 oraz |DC|=13. Oblicz pole trójkąta ABC.
Jakaś wskazówka ?
29 kwi 14:09
jakubs: up?
29 kwi 14:41
J: Rysunek nie zgadza się z treścią.
29 kwi 14:49
jakubs: Oj źle przepisałem

|BC|=13
29 kwi 14:51
J: Jesli BC = 13 i CD = 13 to trójkąt DBC jest równoramienny .. )
29 kwi 15:55
pigor: .., niech CE=h − wysokość względem AB, to
PΔABC= 12*21k*h= ?
gdzie z warunków zadania :h
2=13
2−(5k)
2 i h
2= 20
2−(11k+5k)
2 ⇔
⇔ 13
2−(5k)
2 = 20
2−(11k+5k)
2 i
h2= 169−25k2 ⇒
⇒ (16k−5k)(16k+5k) = (20−13)(20+13) ⇔ 11*21k
2 = 7*33 ⇔
k2=1 ⇒
⇒ h
2=169−25= 144 ⇒
h=12 , więc
PΔABC= 12*21*12= 6*21=
126 j
2. − szukane
pole .
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
przepraszam za gotowiec, ale właśnie "znikam" do wieczora a ...

moja szuflada...

czeka . ...

29 kwi 16:04
jakubs: Dziękuję pigor
Zauważyłem, że jest tam trójkąt równoramienny i wyznaczyłem h
2=169−25x
2, ale nie zauważyłem
tego, że również h
2=400−256x
2 i na tym się zatrzymałem

29 kwi 16:14



 Czas na ostrosłup
Czas na ostrosłup  Dany jest ostrosłup ABCD, w którym podstawa jest trójkąt równoramienny ABC i |AB|=48,
|BC|=|AC|=30, a spodek wysokosci ostrosłupa nalezy do jego podstawy. Każda wysokość ściany
bocznej poprowadzona z wierzchołka S ma długość 17. Oblicz objętość tego ostrosłupa.
Rysunek ok ?
Dany jest ostrosłup ABCD, w którym podstawa jest trójkąt równoramienny ABC i |AB|=48,
|BC|=|AC|=30, a spodek wysokosci ostrosłupa nalezy do jego podstawy. Każda wysokość ściany
bocznej poprowadzona z wierzchołka S ma długość 17. Oblicz objętość tego ostrosłupa.
Rysunek ok ?
 proste.
proste.



 same, ale ...z czasem i tyle . ...
same, ale ...z czasem i tyle . ...
 Oblicz, ile jest liczb naturalnych siedmiocyfrowych, w zapisie których występuje dokładnie trzy
razy cyfra 7, dokładnie dwa razy cyfra 0 oraz dokładnie raz występuje cyfra 1.
Oblicz, ile jest liczb naturalnych siedmiocyfrowych, w zapisie których występuje dokładnie trzy
razy cyfra 7, dokładnie dwa razy cyfra 0 oraz dokładnie raz występuje cyfra 1.
 I znowu planimetria <3
W trójkącie ABC dane sa długości boków |AC|=20 i |BC|=20.Na boku AB leży punkt D, taki ze |AD|
: |DB=11:10 oraz |DC|=13. Oblicz pole trójkąta ABC.
Jakaś wskazówka ?
I znowu planimetria <3
W trójkącie ABC dane sa długości boków |AC|=20 i |BC|=20.Na boku AB leży punkt D, taki ze |AD|
: |DB=11:10 oraz |DC|=13. Oblicz pole trójkąta ABC.
Jakaś wskazówka ?
 |BC|=13
|BC|=13
 moja szuflada...
moja szuflada... czeka . ...
czeka . ... 
