Dowód
Godzio: Dla maturzystów
W trójkącie ABC długości boków wynoszą:
|AB| = c, |AC| = b, |BC| = a, gdzie 0 < a < b < c.
Pole tego trójkąta wynosi 3. Wykaż, że |AC| > √6.
27 kwi 23:30
zawodus: ja tylko po to, abym mógł je łatwo znaleźć

27 kwi 23:43
lotek: Jak to policzyć?

Juz od pół godziny siedzę i nic

28 kwi 00:34
Godzio:
Chyba trudne nie jest, trzeba kombinować

28 kwi 00:36
zawodus: Korci mnie by dać rozwiązanie, ale się powstrzymać

Idę spać

28 kwi 00:41
Hajtowy:
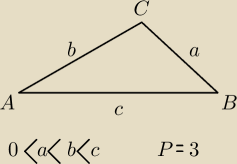
No to tyle mojego w tym zadaniu

28 kwi 10:00
zombi: Obstawiam, że może być coś z sinusami i cosinusami, bo
acsinα = 6, ale więcej nie kombinowałem.
28 kwi 10:39
muflon: zawodus, a jakaś mała wskazówka

28 kwi 14:23
Saizou :
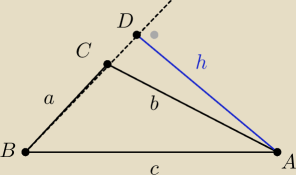
6=ah
b>a
b≥h
====*
b
2>ah
b
2>6
b>
√6
28 kwi 15:32
pigor: ..., kurcze nieźle sobie to wykombinowałeś,
no to jeszcze z kątem np. tak :
−−−−−−−−−−−−−−−−−−−−−−−−−
PΔ=3 ⇔ 12absinγ= 3 i 0<sinγ≤1 ⇔ sinγ= 6ab i 0<6ab≤1 ⇒
⇒ ab ≥6 i b>a /*stronami ⇒ ab2>6a ⇔ b2>6 ⇒ b=|AC|> √6 c.n.w.
28 kwi 15:48
zawodus: Moje rozwiązanie podobne do tego Saizou tylko bez mnożenia nierówności

28 kwi 17:21
Godzio:

28 kwi 17:50

 Juz od pół godziny siedzę i nic
Juz od pół godziny siedzę i nic

 Idę spać
Idę spać 
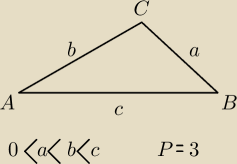 No to tyle mojego w tym zadaniu
No to tyle mojego w tym zadaniu 



