Dla maturzystów Domel: Dla maturzystów Znaleźć liczby p i q takie, aby trójmian kwadratowy x²+px+q dla wartości x spełniających warunek 1<x<5 i tylko dla tych wartości był mniejszy od x

Maslanek: Czyli x²+px+q<x dla 1<x<5 x²+x(p−1)+q<0 f(1)≥0 f(5)≥0

Saizou : Maslanek od kiedy ty jesteś tegorocznym maturzystą

Domel: No i cóż dalej Czy znaki są prawidłowe

Godzio: Trochę mało warunków (równe chyba też nie może być)

zawodus: oczywiście, że mało

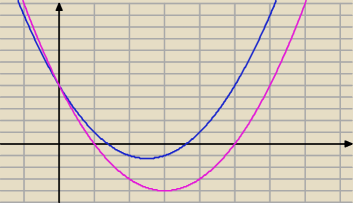
Domel: Przykładowo: Niebieska − f(x) = x² + px + q Fioletowa − g(x) = x² + (p−1)x + q Jakieś wnioski

Maslanek:

	5+1
I standardowo Δ>0 i xw=		=3.
	2

Domel: Z rysunku − dla g(1) i g(5) funkcja f(x) = x x² + px + q = x i co dalej? Jakieś równania, układy równań

Mario:

Mario: Maturzysto!