nierówności kybi: Podaj zbiór rozwiązań nierówności (x+2)(3−x)(x+4)≥

kybi: ≥0

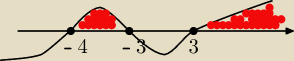
Hajtowy: x=−4 v x=−3 v x=3 to co zakropkowane to rozwiązanie

ICSP: ooo Hajtowy dałeś się złapać

Hajtowy: Serio?

ICSP:

Hajtowy: Od dołu ma iść... Ja tej matury to chyba nie zdam

Hajtowy: w dodatku miejsca zerowe zle napisałem... omg ... chyba mózg już się nie chłodzi

ICSP: Popraw

kybi: Odpowiedź ma byc (−niesk,−4> <−2,3>

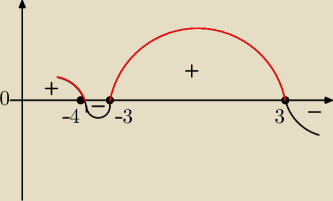
bezendu: (x+2)(3−x)(x+4)≥0 −(x+2)(x−3)(x+4)≥0 / *(−1) (x+2)(x−3)(x+4)≤0 Tak wygląda wykres...

Hajtowy: dzieki bezendu za poprawke

Dziadek Mróz: A jak rozwiązać? Mnie uczono takiego sposobu. Pobierało się wartość x z zakresu zainteresowania i obliczało znak funkcji w tym zakresie: mamy takie zakresy: (−∞, −4>; x = −5; f(−5) = (−5 + 2)(3 + 5)(−5 + 4) = (−)(+)(−) = (−)(−) = (+) <−4, −3>; x = −3.5; f(−3.5) = (−3.5 + 2)(3 + 3.5)(−3.5 + 4) = (−)(+)(+) = (−)(+) = (−) <−3, 3>; x = 0; f(0) = (0 + 2)(3 − 0)(0 + 4) = (+)(+)(+) = (+)(+) = (+) <3, +∞); x = 4; f(4) = (4 + 2)(3 − 4)(4 + 4) = (+)(−)(+) = (−)(+) = (−) f(x) ≥ 0