W okręgu o promieniu r poprowadzono prostopadłe cięciwy... pie: W okręgu o promieniu r poprowadzono prostopadłe cięciwy AB i CD. Wykaż, że |AC|²+|BD|²=4r².

Jurek z matfiz:): zadanie z probnej matury poziom podst.

pie: Zbiorek twierdzi, że to jednak rozszerzenie.

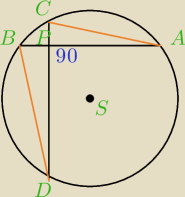
pie: Od czego zacząć?

Marcin: To jest na pewno z rozszerzenia Popatrz też na sposób Ety

Marcin: https://matematykaszkolna.pl/strona/3871.html

Marcin: Oj nie, to nie to

pie: Jakiś pomysł? Nic tu nie widzę.

pomocnik: Wykorzystać tw. sinusów do trójkątów ABD i ACD

pie: Faktycznie da radę, ale niestety nie miałem jeszcze tego twierdzenia na lekcji, dlatego myślę, że musi być jeszcze inny sposób.

pomocnik:

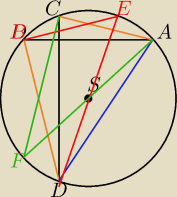
	x
|BD|=x, β=|∡DEB|=|∡DAB|, |∡DBE|=90. Z trójkąta DEB, mamy		=sin β
	2r

Podobnie

	y
|AC|=y, γ=|∡CDA|=|∡CFA|, |∡ACF|=90. Z trójkąta ACF, mamy		=sin γ
	2r

Oczywiście β+γ=90 Czyli x=2r*sin β, y=2r*sin γ=2r*sin (90−β)=2f*cos β. Stąd x²+y²=4r²

pomocnik: x=2r*sin β, y=2r*sin γ=2r*sin (90−β)=2r*cos β.

hubi: oznaczenia: α=|∡CDA|=|∡ADP| 90−α=|∡BAD|=|∡DAP| z pitagorasa i twierdzenia sinusów mamy √|PA|² + |PC|² = 2R*sinα oraz √|PD|² + |PB|² = 2R*sin (90−α)=2R*cosα ale po podniesieniu do kwadratu obydwóch równości mamy: |PA|² + |PC|² = 4R²*sin²α |PD|² + |PB|² = 4R²*cos²α teraz sumując stronami: |PA|² + |PC|² + |PD|² + |PB|² = |AC|²+|BD|²=4R²*sin²α + 4R²*cos²α =4R²(sin²α + cos²α)=4R²