rownania 1-szego stopnia z 2 niewiadomymi
ełt:
Zilustruj zbiór wszystkich punktów płaszczyzny, których współrzędne spełniają równanie:
a) xy = 2y
b) lx + yl = 2
c) l2xl = lx − 2+ yl
27 kwi 19:50
ełt: Up
27 kwi 20:04
ełt: up
27 kwi 20:09
zawodus: xy=2y ⇔xy−2y=0 ⇔y(x−2)=0 ⇔y=0 ∨ x=2
dwie proste.
27 kwi 20:11
PW:
Np.a)
Gdy y = 0, to równanie jest spełnione przez każdą liczbę x, jest to więc równanie
− równanie prostej poziomej.
Gdy y≠0, to dla dowolnej takiej y równanie jest równoważne równaniu
−równanie prostej pionowej "stojącej w punkcie 2".
27 kwi 20:12
PW: zawodus, przepraszam, mam tendencję do gadulstwa i zanim napisałem swoją odpowiedź, to nie
mogłem widzie Twojej

27 kwi 20:13
ełt: Czyli np. :
(x+5)(x−3)=0
x = −5 lub x = 3
To jakby szukanie miejsc zerowych?
A z wartością bezwzględną to najpierw na przypadki?
x+ y = 2 lub x + y = − 2
27 kwi 20:15
ełt: PW, a prościej?

27 kwi 20:16
Nieuchwytny:
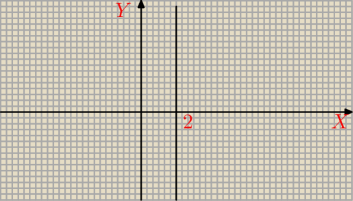
Jeżeli x=2 a y=0 to wygląda tak:
27 kwi 20:19
ełt: Ok, wykres rozumiem, ale jak dojść do reszty?

27 kwi 20:22
Nieuchwytny:
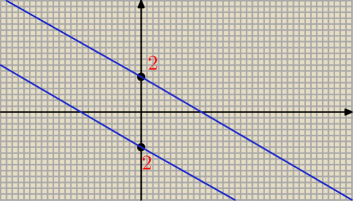
27 kwi 20:23
PW: Nie można prościej, i tak niedbale opisałem drugi przypadek − powinno być "prosta stojąca w
punkcie x=2, bez punktu (2,0)". Po narysowaniu jest tak jak pokazuje Nieuchwytny − dwie
krzyżujące się proste, jednej nie widać, bo pokrywa się z osią OX.
Dlaczego tak piszę? Bo formalnie równanie prostej jest równaniem dwóch zmiennych. Z
doświadczenia wiem, że bardzo wielu uczniów nie widzi równania prostej w napisie y=0 czy x=2,
zapominając o "cichej umowie", że jeśli jednej ze zmiennych nie ma, to oznacza że jest ona
dowolna.
27 kwi 20:27
analny sandał :
big black cock
8 paź 11:36
5-latek: Nie masz co robic to idz sobie umyj nogi bo ci smierdza
8 paź 11:43


 Jeżeli x=2 a y=0 to wygląda tak:
Jeżeli x=2 a y=0 to wygląda tak:


 big black cock
big black cock