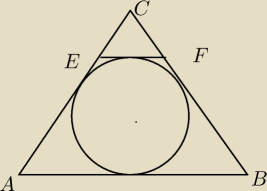
Dowód muflon: Niech to będzie trójkąt równoramienny. EF jest równoległe do AB EF styczne do okręfu wpisanego w ten trójkąt. Wykaż, że: Pole trójkata to : [IABI²*√IABI*IEFI]/[2(IABI−IEFI)] Proszę o pomoc

zawodus: Co jest dane w tym zadaniu? Napisz porządnie treść tego zadania

muflon: właściwie to fakt, że to jest tr równoramienny okrąg wpisany, a EF styczne do okręgu i równoległe do AB

zawodus: z tego co piszesz to nic nie wynika. Jak nie umiesz zacytować zadania, to daj linka skąd je masz

muflon: "Na ramionach AC i BC trójkąta równoramiennego ABC obrano E i F tak, że EF jest równoległe do AB−podstawy i styczny do okręgu wpisanego w trójkąt. Wykaż że P tr = [AB²*√AB*EF]/[2(AB−EF)]

zawodus: Ja mam, a ty? Piękne zadanie

muflon: wysokość małego trójkąta wyszła mi: a* (sinα(1−cosα)/(1+cosα) a− ramię, α kat przy podstawie, dobrze?

zawodus: Tylko, że kąta nie mamy danego. staraj się uzależnić dane od tego co mamy, czyli podstaw trapezu

muflon: No ale z 2 strony: P= a²/2 * sin 2α Udowadniejąc to przecież możemy dojąć do pola

zawodus: dobrze to przedstaw swoje rozwiązanie, a ja wtedy powiem czy ok

muflon: *dojść

muflon: to na razie mam tak: a, ramiona α kąt przy podstawie podstawa 2*acosα wysokość a*sinα P=a²/2*sin2α r=P/p p− polowa obwodu r=a(sinαcosα/1+cosα) wysokość małego trójkąta: a*sinα−2r=.... teraz z podobienstwa licze połowę EF i potem EF Potem podstawiam

zawodus: pytanie, czy otrzymujesz wynik podany w zadaniu?