ciągi
Piotruś: | | (−1)n*2n | |
Dany jest nieskończony ciąg an= |
| . |
| | n+3 | |
a)Wykaż, że nie istnieje granica ciągu.
b)Wyznacz największą liczbę a i najmniejszą liczbę b, dla których każdy wyraz an ciągu spełnia
warunek: a ≤ an ≤ b.
Proszę powiedzcie mi tylko jak zapisać ciąg jako parzysty lub nieparzysty bo wiem że trzeba to
zrobić? Może mi się uda wtedy to zrobić.
27 kwi 17:03
sushi_ gg6397228:
w klamerce
| | ⎧ | .... dla n =2k, k ∊ N+ | |
| | ⎩ | .... dla n =2k+1, k ∊ N+ |
|
27 kwi 17:10
Piotruś: Ach, już zczaiłem o co chodzi z tą parzystością. Dzięki za odp. A jak zrobić b?
27 kwi 17:28
sushi_ gg6397228:
policz dla pierwszych 10 wyrazów, jaki będzie znak ciągu
27 kwi 17:31
Piotruś: Dobra już chyba wiem. W odpowiedzi a=−2 natomiast b=2, czyli to są granice podciągów parzystego
i nieparzystego, które mi wyszły w pkt a). Dziwne to zadanie trochę.
27 kwi 17:48
sushi_ gg6397228:
jakby nie było minusa, to granica jest "2",
jest minus, wiec ciąg dąży do "2" i "−2"
27 kwi 17:52
Piotruś: Ok. Dzięki

27 kwi 17:56
matematyk: Ja niestey nie rozumiem o co chodzi z tą nieparzystością. Mógłby ktoś mi wyjaśnić? Z góry
dziękuję

11 maj 11:02
J:
zapis: n = 2k − oznacza wyraz parzysty i wtedy : (−1)n = 1
n = 2k+1 − oznacza wyraz nieparzysty i wtedy : (−1)n = −1
11 maj 11:05
matematyk: I teraz dla każdeg ciągu policzyć lim?
11 maj 19:43
matematyk: Bo wtedy mi wychodzi, że dla parzystych lim=2 a dla nieparzystych lim=−2. Tylko co dalej

11 maj 19:46
@: Jeżeli dla nieparzystych wychodzi inna granica niż dla parzystych, to nie ma jednej (wspólnej)
granicy dla tego ciągu

11 maj 20:45
matematyk: Wydawało mi się, że to nie może być takie proste. Dziękuję za pomoc

11 maj 22:08
matma: a jak zrobić podpunkt b?
24 maj 17:06
Adamm:
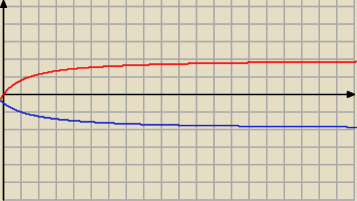
b)
rozbijamy na dwa ciągi
wiemy jak wygląda funkcja homograficzna
dla a
2k mamy rosnącą funkcję która dąży asymptotycznie do 2
zatem a
2≤a
2k≤2
za to dla a
2k+1 mamy malejącą która dąży do −2
zatem −2≤a
2k+1≤a
1
ostatecznie −2≤a
n≤2
24 maj 17:17





 b)
b)