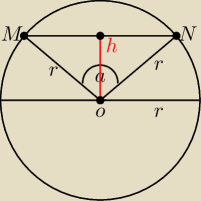
 W jakiej odległości od środka półkola o promieniu r należy poprowadzić cięciwę MN równoległą do
średnic, aby po połączeniu końców MN z O otrzymać trójkąt o największym polu.
W jakiej odległości od środka półkola o promieniu r należy poprowadzić cięciwę MN równoległą do
średnic, aby po połączeniu końców MN z O otrzymać trójkąt o największym polu.
| |MN|*h | ||
PΔOMN= | ||
| 2 |

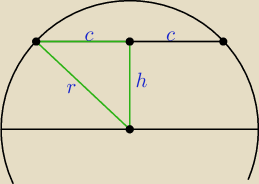 c = √r2 − h2, pole P = c*h = √r2 − h2 * h
Trzeba wyznaczyć h, dla którego funkcja P(h) = √r2 − h2 * h osiąga maksimum
c = √r2 − h2, pole P = c*h = √r2 − h2 * h
Trzeba wyznaczyć h, dla którego funkcja P(h) = √r2 − h2 * h osiąga maksimum
 Dzięki wielkie
Dzięki wielkie 