Prośba o wytłumaczenie :) Ciekawska: Wytłumaczyłby mi ktoś jeszcze raz jak wyliczyć punkt układu współrzędnych, który nie jest podany? Chodzi mi o równania prostej przechodzącej przez dwa punkty . Np. mam policzyć trójkąt, a podano mi 2 punkty albo równoległobok, gdzie mam dane 3.

Tadeusz: ... to może zapisz zadanie −

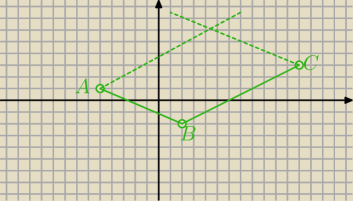
Ciekawska: W równoległoboku ABCD dane są trzy wierzchołki: A(−5,1), B(2,−2) i C(12,3). a) napisz równania prostych, w których zawierają się boki równoległoboku b) wyznacz równanie prostej, zawierającej wysokość poprowadzoną z wierzchołka D na bok AB Więc: AB II DC BC II AD y = ax + b Prosta AB −> y = −3/7 x − 8/7 Prosta BC −> 1/2 x − 3 AD y = 1/2 x + b

Ciekawska: O ile 2 pierwsze proste mogę wyliczyć bez problemu, używając układu równań, to, przy AD i CD nie wiem co zrobić .

Tadeusz: ... prosta równoległa do danej prostej i przechodząca przez punkt −

Ciekawska: Skoro prosta AD jest równoległa do prostej BC, to musi mieć ten sam współczynnik kierunkowy a, czyli 1/2 x Pytanie jak wyliczyć b? .

Tadeusz:

Alfa: z faktu, że pr. AD przechodzi przez punkt A

Ciekawska: Też to sobie narysowałam w zeszycie . Nie potrafię obsługiwać się rysunkami tutaj, bo wychodzą mi malutkie kratki. Tyle, że punkt D wychodzi gdzieś pomiędzy (x, 6), gdzie x jest pomiędzy 4 a 5 .

Ciekawska: *Tyle, że punkt D wychodzi (x, 6), gdzie x jest pomiędzy 4 a 5 .

Ciekawska: Alfa, i co mam z tym faktem zrobić? Naprawdę tego nie rozumiem.

Tadeusz:

	3+2		1
Prosta przez B i C to y−3=		(x−12) y=		x−3
	12−2		2

	1
Prosta przez A i D to y−1=		(x+5)
	2

Tadeusz: ta prosta ma współczynnik kierunkowy 1/2 i przechodzi przez A Wiemy, że punkt D na niej leży (nie znając obu współrzędnych) Punkt D wyznaczysz z przecięcia się prostych

Ciekawska: To wygląda strasznie . Nawet nie wiem jak do tego doszedłeś.

Tadeusz: ... przypomnij sobie równanie pęku prostych przez dany punkt −

Ciekawska: Na rysunku to widać, ale jak to zapisać? Do miejsca o współczynniku kierunkowym rozumiem, ale o b nie jestem w stanie nic powiedzieć .

Ciekawska: (x₂ − x₁)(y − y₁) = (y₂ − y₁)(x − x₁) To?

Tadeusz: Masz punkt A Przez ten punkt możesz poprowadzić pęk prostych y−y_A=a(x−x_A) a z tego bezliku prostych wybierasz tą która ma a=1/2 czyli y−1=1/2(x+5)

Tadeusz: coś się uparła do tego "b" ... chyba lubisz "be" −

Tadeusz: a to co napisałaś to równanie prostej przez dwa punkty a nie równanie pęku prostych −

Ciekawska: Ale ja czegoś takiego nie miałam na lekcjach . Nie da się tego zrobić w inny sposób?

Tadeusz: pewnie że się da ... jak wszystko w matematyce −) Pokaże Ci to samo a nie to samo −

Ciekawska: Okej, dziękuję . Da się to zrobić np. na układzie równań albo poprzez równanie prostej przechodzącej przez dwa punkty?

Tadeusz: Piszemy równanie prostej przez A i D ... współrzędnych D nie znamy

	yA−yD
y−yA=		(x−xA)
	xA−xD

tego co w ułamku policzyć nie umiemy ... ale i nie musimy bo to współczynnik kierunkowy który już znamy −

Tadeusz: Pani Ciekawska ... zachęcam do "opanowania" równania pęku przez dany punkt −

Ciekawska: Cóż, Wy, matematycy i fizycy już tak macie, że wszystko dla Was jest proste i lubicie utrudniać sobie życie, używając ogromnych wzorów . Opanuję chociażby we wtorek, ale dzisiaj na prawdę nie jestem w stanie zapamiętać tego wzoru .

Tadeusz: przecież wzór na równanie prostej przez dwa punkty napisałaś − A ten na równanie pęku wynika z jego przekształcenia. A ja nie jestem matematykiem ... tylko meblarzem −

Ciekawska: Bo jakoś lepiej układa mi się w głowie . Serio, mam dość, od 13 siedzę nad 3 zadaniami o wspólnym mianowniku. A przede mną jeszcze 120 zadań . Ale matematyka dobrze Ci idzie, czyżby hobby?

Tadeusz: ... a lubię −

Ciekawska: No dobrze, więc co z tym zadaniem? Zapodasz jakiś inny sposób?

Tadeusz: ... przecież podałem Ci − ... nie czytasz Oczywiście można to zrobić na jeszcze kilka sposobów ...

Ciekawska: Czytam . (x₂ − x₁)(y − y₁) = (y₂ − y₁)(x − x₁) No to AD A(−5,1) (x₂ + 5)(y − 1) = (y₂ − 1)(x + 5) I to nic mi nie da, bo będę mieć skomplikowane wyrazy, np. x₂y, y₂x

Ciekawska: A da się to zrobić za pomocą układu równań, skoro znam współczynnik kierunkowy?

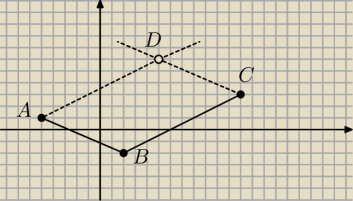
Dziadek Mróz: A(−5,1), B(2,−2) i C(12,3) prosta AB:

⎧	yA = axA + b
⎩	yB = axB + b

y_AB = a_ABx + b prosta BC:

⎧	yB = axB + b
⎩	yC = axC + b

y_BC = a_BCx + b prosta AD:

⎧	yA = aBCxA + b
⎩	yD = aBCxD + b

b będzie równe np. b = y_D + 2x_D prosta CD:

⎧	yC = aABxC + b
⎩	yD = aABxD + b

b będzie równe np. b = 2y_D + 3x_D y_AD = y_CD z tego wyjdzie x_D i y_D D = (x_D, y_D)

Tadeusz: zauważ, że punkt D należy zarówno do prostej przechodzącej przez A i D jak i przechodzącej przez C i D. Skoro należy ... to spełnia równania tych prostych Tak doprowadzisz do układu dwóch równań z których wyznaczysz x_D i y_D (tyle, że to trudniejszy sposób)

olek2345: Okej, a najprostszym ze sposobów jak by to wyglądało? Dziadku Mróz, nie jestem w stanie tego zapamiętać . Aczkolwiek Twój sposób jest przejrzysty. Dziękuję .

Dziadek Mróz: Mój sposób jest najprostszy bo łatwy do zapamiętania. Skojarzyć, że wzór prostej przechodzącej przez dwa punkty to układ równań ze współrzędnymi tych punktów.

olek2345: Rzeczywiście I ma on zastosowanie do wszystkich zadań tego typu?

olek2345: To teraz podstawiam i zobaczymy co z tego wyjdzie

Ciekawska : Hm

	1
1 =		* −5 + b
	2

	1
yD =		xD + b
	2