matematyka
kyrtap:
ARKUSZ 1 (27 kwietnia rok 2014 godzina 16:13)
1. Zbadaj wzajemne położenie prostej określonej równaniem y = x +m i okręgu o równaniu
x
2 + y
2 = 9 w zależności od parametru m.
| | 2 | |
2. Dla jakich wartości m reszta z dzielenia wielomianu W(x) = x3 − |
| x2 + mx −2 przez |
| | m | |
dwumian x − 2 jest mniejsza lub równa 6?
3. Wielościan jest sumą dwóch ostrosłupów prawidłowych czworokątnych o długościach wszystkich
krawędzi równych 10 cm i złączonych podstawami (ośmiościan foremny). Wielościan ten przecięto
płaszczyzną równoległą do dwu przeciwległych jego ścian i przechodzącą przez środki krawędzi
nie zawierających się w tych ścianach. Oblicz pole otrzymanego przekroju. Wynik podaj z
dokładnością do 0.01cm
2.
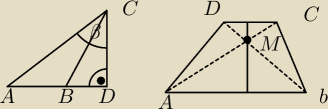
4.Na rysunku przedstawiono trzy trójkąty w tym równoramienny trójkąt ABC ( o podstawie AC) oraz
| | 1 | |
prostokątny równoramienny trójkąt BDC ( o podstawie BC). Uzasadnij, że cos(∡ACD)< |
| . |
| | 2 | |
5. Przekątne trapezu ABCD przecinają się w punkcie M. Wysokość trapezu ma długość 18. Pole
trójkąta ABM jest równe 25, pole trójkąta CDM jest równe 16. Oblicz pole trapezu.
6.Na loterii fantowej wśród n losów jest 6 losów wygrywających.Oblicz n,dla którego
| | 1 | |
prawdopodobieństwo zdarzenia,że kupione 2 losy są wygrywające jest większe od |
| . |
| | 3 | |
7. Podaj odpowiednie założenie i wykaż, że
| | sin(α+β)sin(α−β) | |
tg2α − tg2β = |
| . |
| | cos2 α * cos2 β | |
8. Funkcja f jest określona wzorem f(x) = log
2 x
a) Oblicz miejsce zerowe funkcji g(x)=−f(x−3)+2 i sporządź jej wykres.
b) Podaj liczbę rozwiązań równania |g(x)|=m w zalezności od parametru m.
9.Liczbę 147 przedstaw w postaci sumy siedmiu składników, tak aby te składniki były kolejnymi
wyrazami ciągu arytmetycznego i aby ostatni składnik był sześć razy większy niż pierwszy.
Oblicz te składniki.
10.Zbiór A jest zbiorem liczb spełniających równanie Ix−1I+Ix−3I=2 a zbiór B jest zbiorem
współrzędnych wszystkich punktów na osi liczbowej,których odległość od liczby 5 jest nie
mniejsza niż 3.Zaznacz na osi liczbowej zbiory A i B oraz wszystkie punkty,których współrzędne
należą do zbioru A i jednocześnie do B.
(rysunki są do zadań 4 i 5)
27 kwi 16:13
Marcin: Skąd to masz? Zadania.info?

27 kwi 16:15
kyrtap: nie nie zadania info

27 kwi 16:26
Marcin: Ok, to później się za nią wezmę

27 kwi 16:29
kyrtap: jak będzie się komuś chciało to robić to podam wieczorem odpowiedzi
27 kwi 16:29
kyrtap: dobra luz więc wbiję potem a teraz spadam z komputerka bye

27 kwi 16:29
Marcin: Jak tam wyniki z wczorajszej maturki?
27 kwi 16:29
Marcin: No Cya

27 kwi 16:30
kyrtap: 60%

27 kwi 16:30
Marcin: Nie jest źle

Ja miałem prawie 80

27 kwi 16:31
kyrtap: no to nie mamy o czym rozmawiać Marcinie
27 kwi 16:32
kyrtap: 
27 kwi 16:32
Marcin: Na głównej napiszesz lepiej ode mnie!

27 kwi 16:33
kyrtap: Jak nie napiszę zgaduję się z Tobą na skype i pijemy

27 kwi 16:34
Marcin: Przez Skype'a jeszcze nie piłem

a gdzie mieszkasz, co?

27 kwi 16:50
kyrtap: Szczytno
27 kwi 16:53
Marcin: Takie tam 600km do mnie

27 kwi 16:54
kyrtap: a ty?
27 kwi 16:56
Marcin: Okolice Przemyśla

27 kwi 17:07
kyrtap: hoho kawałek jest
27 kwi 17:10
Marcin: 1:
x
2 + y
2 = 9
x
2 + (x +m)
2 = 9
2x
2+2mx+m
2−9=0
Δ≥0 ← warunek, żeby były punkty wspólne.
4m
2−4(2m
2−18)≥0
4m
2−8m
2+72≥0
4m
2≤72
m
2≤18
Prosta ma punkty wspólne z okręgiem dla m∊ <−
√18;
√18>
Beje good?

27 kwi 21:05
Marcin: 2:
Dzielę wielomian Hornerem i mam coś takiego:
Czyli:
−8m+2m
3≤0
Z tego:
m∊(−
∞;−2> ∪ (0;2>
27 kwi 21:13
Saizou : Marcin a tw. o reszcie z dzielenie wielomianu przez dwumian znasz

27 kwi 21:15
Marcin: Na jedno wychodzi

27 kwi 21:17
Saizou : wiem, ale szybciej jest trochę xd
27 kwi 21:18
Marcin: oj tam. Jak nie będę wiedział jak robić inne zadania na maturze, to się Hornerem pobawię

27 kwi 21:20
zawodus: Łaiwiej się pomylić
27 kwi 21:22
Marcin: Ok, przekonałeś mnie

27 kwi 21:25
zawodus: Co nie znaczy, że Herona nie warto używać

W przypadku wielomianów, gdzie dzielimy i ma wyjść 0 to jest super szybki sposób

27 kwi 21:27
zawodus: tzn jak mamy liczby bez parametrów

27 kwi 21:28
Marcin: Ja tam lubię Pana Herona

nie lubię za to grupowania

27 kwi 21:33
kyrtap: Haj haj

27 kwi 21:54
kyrtap: Marcin znasz tw Bezouta? Czemu nie stosujesz?
27 kwi 21:56
Saizou : kyrtap a gdzie chcesz je wcisnąć ?

27 kwi 21:59
kyrtap: w zadaniu 2?
27 kwi 21:59
kyrtap: Czy to nie to twierdzenie

27 kwi 22:00
Marcin: Z tym wielościanem, to nie mam pewności, ale to chyba będą dwa trapezy równoramienne nałożone
na siebie.
P=15*√31,25, coś takiego?
27 kwi 22:00
Saizou : a co mówi Pan Bezout?

27 kwi 22:01
Marcin: Wynik się zgadza?

Mi to podzielenie hornerem zajęło dosłownie 30 sekund. Ja nie wiem gdzie
wy tutaj problem widzicie

27 kwi 22:01
Marcin: Kyrtap z Beoutem wódkę pił

27 kwi 22:02
kyrtap: Nie wiem nie uczę się tw. na pamięć

ale coś o pierwiastkach zapewne
27 kwi 22:04
kyrtap: no kiedyś

27 kwi 22:04
kyrtap: Def:
Liczba r jest pierwiastkiem wielomianu W(x) ⇔ W(x) jest podzielny przez dwumian (x−r).
27 kwi 22:06
kyrtap: To miałem zanotowane w zeszycie

27 kwi 22:07
Saizou : Tw. Bezout mówi o tym że jeśli liczba a jest pierwiastkiem wielomianu to wielomian dzieli się
przez dwumian x−a. I odwrotnie

27 kwi 22:07
Marcin: Ten trójkąt BDC nie wygląda u Ciebie na równoramienny

27 kwi 22:08
Saizou : czyli to co masz zapisane, a ja podkreślę to że jest
pierwiastkiem 
27 kwi 22:08
kyrtap: sorry bo na szybkiego rysowałem a tutaj nie umiem też za bardzo rysować
27 kwi 22:09
kyrtap: Krótka definicja nie ? A ja jej nie umiem xd
27 kwi 22:09
Marcin: Czyli z polskiego na nasze: Jak sobie wstawisz pierwiastek za x do wielomianu, to nie
dostaniesz reszty

27 kwi 22:09
Saizou :
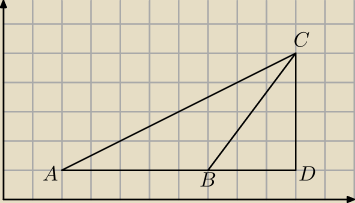
a teraz pasuje

27 kwi 22:10
kyrtap: no cholera Marcin nie ma takiej opcji

27 kwi 22:10
Saizou : czepiacie się

to był tylko rysunek poglądowy

27 kwi 22:23
kyrtap: ten mój?
27 kwi 22:24
Marcin: Jakiej nie ma opcji?

27 kwi 22:25
Marcin: Jak tam dalej nie widzę trójkąta równoramiennego

27 kwi 22:25
kyrtap: Marcinek nie denerwuj mnie

27 kwi 22:27
Saizou :
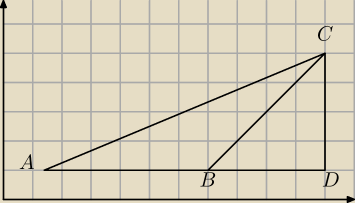
i się nie kłóćcie

27 kwi 22:34
zombi: Siadam do niej

27 kwi 22:34
kyrtap: jutro wam dodać następny czy nie chce się wam robić?
27 kwi 22:35
Saizou : zombi za łatwa jak dla Ciebie

27 kwi 22:36
zombi: Wrzucaj, wrzucaj. Tydzień+ do matury, zaczynamy się uczyć

27 kwi 22:36
kyrtap: Saizou aż taka prosta dla Ciebie?
27 kwi 22:37
zombi: Saizou nie gadaj, ja nie potrafię nic z planimetrii.
27 kwi 22:38
Saizou : ja nie mówiłem że prosta dla mnie, tylko że dla zombiego xd
27 kwi 22:38
Marcin: Dla Saizou też

27 kwi 22:39
kyrtap: Widzę że każdy jest dobry oprócz mnie xd
27 kwi 22:39
Saizou : Marcin co ty za bzdury opowiadasz, gdzie dla mnie prosta

27 kwi 22:41
Marcin: Kto Ci powiedział że jesteś słaby? (oprócz Ciebie)

27 kwi 22:41
Marcin: Patrz jak jeszcze ironią jedzie

27 kwi 22:41
Marcin: Ile wam wyszło w tym 3, co?
27 kwi 22:42
kyrtap: bo tak patrzę jak wszystko na lajcie rozwiązujecie
27 kwi 22:42
Marcin: Wczoraj to Ty zrobiłeś dobrze zadanie, a ja nie wiedziałem jak je ogarnąć

27 kwi 22:45
kyrtap: To był mój pierwszy raz

27 kwi 22:45
Saizou : szczerze mówiąc to jeszcze nie liczyłem żadnego zadanka z tego arkusza

zaraz to zobaczę

27 kwi 22:46
zawodus: Teraz już z górki

27 kwi 22:46
Marcin: Ja się często mylę

Chociaż nie powiem, są tu niektórzy mocno ogarniający

27 kwi 22:46
Marcin: Zawodus, musiałeś być dobry w 'skojarzenia'

27 kwi 22:47
kyrtap: Ty też jesteś kozak więc nie bądź taki skromny

27 kwi 22:47
Marcin: Pochwalimy się sobie później wynikami z matury i zobaczymy kto jest kozakiem

27 kwi 22:50
kyrtap: ja będę kmieciem

27 kwi 22:51
Marcin: Kmieć (łac. cmetos, cmetonis, kmetho) – w czasach nowożytnych pojęcie to oznacza zamożnego
gospodarza

27 kwi 22:53
zombi: Jak to w trzecim ma wyglądać ? XD
27 kwi 22:54
Marcin:
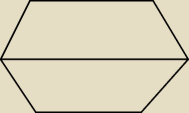
Według mnie tak

(w sensie przekrój)
27 kwi 22:56
zawodus: dobra widzę, że się nudzicie

zadania

1. Wyznacz zbiór wartości funkcji
f(x)= cosx
√(1+tg2x)
oraz drugie
| | 4 | |
2. Wyznacz zbiór wartości funkcji f(x)= |
| |
| | | |
27 kwi 23:01
Saizou :
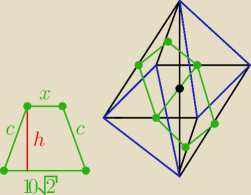
27 kwi 23:01
Marcin: No jak się nudzimy, jak robimy tą maturkę z góry?

27 kwi 23:02
Marcin: Saizou dlaczego w podstawie masz 10√2? Przecież krawędź podstawy ma 10..
27 kwi 23:03
Saizou : tak miało być 10, najwidoczniej jak rozważałem opcje to tego nie wykasowałem xd
27 kwi 23:04
Marcin: rozważałeś inne opcje, rozumiem

27 kwi 23:05
kyrtap: Saizou tysiąc sposobów rozwiązania na sekundę

27 kwi 23:05
zombi: Ok to liczę ten przekrój, Marcin podaj swoją odp. jak coś.
27 kwi 23:05
Marcin: Według mnie c=x=5.
27 kwi 23:05
Saizou : aż tak wydajny to ja nie jestem

rozważałem inną opcję przez głupotę

27 kwi 23:06
Marcin: Podałem,
P= 15
√31,25 =83,25 cm
2, ale nie wiem czy jest ok i mi nikt nie chce potwierdzić

27 kwi 23:07
Marcin: 83,85*
27 kwi 23:07
kyrtap: już patrzę do zbioru
27 kwi 23:07
zawodus: Wg mnie też x=5 i c=5

27 kwi 23:08
zawodus: kyrtap z jakiego to zbioru?

27 kwi 23:08
27 kwi 23:09
zombi: Marcin a nie czasem 15√18,75 ?
Bo z Pitka mamy
h2 + (2,5)2 = 52
27 kwi 23:09
kyrtap: Podkowa
27 kwi 23:09
Marcin: Pewnie, pewnie. Poryłem się i zamiast 5
2−(2,5)
2, to ja to dodałem

27 kwi 23:10
Marcin: Ale bym się wkurzył jakbym taki błąd walnął na maturze

27 kwi 23:11
Marcin: Wtedy nawet wynik od kyrtapa powinien się zgadzać

27 kwi 23:12
Piotr 10: Zad 5/
Ptr=(√P1 + √P2))2 = 25 +16 * 2*16*25=81
.
27 kwi 23:13
Marcin: Tam jeszcze nie doszedłem. Cześć Piotrek

27 kwi 23:14
Saizou : to było zadanie z podkowy ?
27 kwi 23:14
Piotr 10: Witaj, ja tylko jedno sobie zrobilem z ciekawosci

27 kwi 23:14
kyrtap: tak Podkowa
27 kwi 23:15
zawodus: Piotrek wzorek, którego użyłeś należałoby wykazać na maturze raczej

27 kwi 23:17
Piotr 10: spoko moge go wykazac jesli ktos chce
27 kwi 23:18
zombi: Z podobieństwa i skali podobieństwa wystarczy.
27 kwi 23:19
zombi: Pokaże, ktoś 4? Bo chciałbym zobaczyć czy podobnie.
27 kwi 23:19
Piotr 10: No ja wiem, ale tak naprawde nie potrzebna jest wysokosc w tym zadaniu ( nadmiar danych )
27 kwi 23:19
Marcin: Piotrek też mam taki wynik, tylko że inaczej chyba liczyłem

27 kwi 23:19
Marcin: Ciekawy jestem czy za Twoje rozwiązanie dostałbyś maxa

27 kwi 23:21
Saizou :
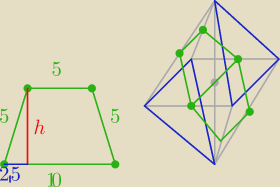
wynika to np. z tw. talesa
| | 1 | | 5√3 | | 75√3 | |
Pp=2*Pt=2* |
| *(5+10)* |
| = |
| |
| | 2 | | 2 | | 2 | |
27 kwi 23:21
zombi: Ja bym na początku napisał, że trójkąty te dwa są podobne, następnie, że P1 = k2 * P2,
wyliczyłbym skalę podobieństwa, pokazał, że te małe po bokach są podobne do największego w
skali k i wtedy liczył pole całego jako
Pc = (k+1)2*P1. Na maturze bym tak rozpisywał, żeby max był.
27 kwi 23:23
Marcin: | | 5 | |
Skala podobieństwa to |
| , więc: |
| | 4 | |
9x=18
x=2
wysokości trójkątów to 10 i 8 ← z tego policzyłem podstawy i też jest ok

27 kwi 23:25
Piotr 10:
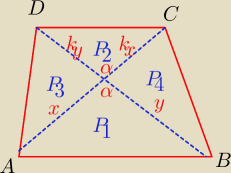
Przekątne trapezu ABCD przecinają się w punkcie M. Wysokość trapezu ma długość 18. Pole
trójkąta ABM jest równe 25, pole trójkąta CDM jest równe 16. Oblicz pole trapezu.
P
3=P
4
P
tr=P
1+P
2+P
3+P
4 = P
1+P
2+2P
3
| | 1 | |
P3= |
| *xyksinα a zatem ( wniosek) |
| | 2 | |
P
3=
√P1*P2 , gdyż
Więc:
P
tr=P
1+P
2+2
√P1*P2= (
√P1+
√P2 )
2
27 kwi 23:26
Saizou :
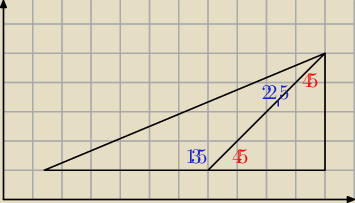
cos(45+22,5)=cos(67,5)
| | 1 | |
a skoro cosinus w przedziale <0:90o> maleje to cos(67,5)<cos(60)= |
| |
| | 2 | |
27 kwi 23:26
Marcin: Saizou dobre, dobre. a ja jakoś beznadziejne kombinowałem

27 kwi 23:27
Saizou : maleje w większym przedziale ale ten kąt może być tylko z przedziału (0:90)

27 kwi 23:28
Mila:
zadanie 5)
P
ΔCMB=P
ΔAMD=x
P
trapezu=2*20+16+25=81
27 kwi 23:30
zombi:
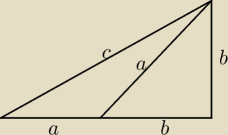
Ew. można tak:
a=
√2b
więc a+b = (
√2+1)b
Z tw Pitagorasa policzyć c i wtedy.
Ale to taki drugi sposób, żeby był. Saizou lepszy.
27 kwi 23:31
Marcin: Robiłem tak jak zombi. Piona

27 kwi 23:33
kyrtap: Mam pytanko do was? Czy może ktoś przerabiał arkusze podstawowe z matur poprzednich?
27 kwi 23:36
kyrtap: w sensie majowych
27 kwi 23:37
zombi: Jakie nki wam wyszły w tym prawdo?
Ja nie

nie opłaca się moim zdaniem.
27 kwi 23:39
kyrtap: ok więc też nie będę robił

27 kwi 23:40
zawodus: Ja znam wszystkie, a o co chodzi?

27 kwi 23:40
Saizou : może kiedyś na zabicie czasu

ale już nie pamiętam, chyba z maja 2013 xd
w zadaniu 9 przyjemnie oznaczyć te wyrazy ciągu jako
a
1=x−3r
a
2=x−2r
a
3=x−r
a
4=x
a
5=x+r
a
6=x+2r
a
7=x+3r
27 kwi 23:41
kyrtap: zawodus dla nas tu obecnych jedynie chyba mogą być problemowe te zadania dowodowe co?
27 kwi 23:43
zombi: Lećcie po kolei

Bo ja chce wyniczki sprawdzać. W prawdo jak macie?
Tożsamość trygo łatwa.
27 kwi 23:44
Marcin:
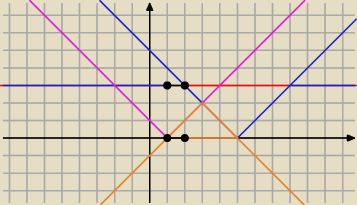
Zad 10:
Ix−1I=2−Ix−3I
|x−5|≥3
x∊<1;2>
Lubię robić graficznie takie zadania, mam nadzieję, że jest ok

27 kwi 23:44
Marcin: Ja prawdopodobieństwa nawet nie ruszam, nie ogarniam

27 kwi 23:45
Mila: 6) n∊{6,7,8,9}
27 kwi 23:46
Marcin: kyrtap rób majowe. One są dość proste, ale przynajmniej z poziomem CKE się zaznajomisz

27 kwi 23:46
zawodus: Akurat to jest banalne

27 kwi 23:47
zombi: Dzięki Mila, to samo!

27 kwi 23:47
Saizou :
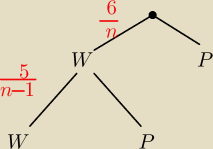
zad. 6
zasadźmy drzewka

W− wygrana
p− przegrana
n∊N
+ i n≥6
90>n(n−1)
n
2−n−90<0
(n−10)(n+9)<0
n∊(−9:10) i D
n∊{6,7,8,9}
27 kwi 23:47
kyrtap: w dzień jutro wszystkie przerobię i do podstawy będę przygotowany formalnie

27 kwi 23:48
Marcin: Ty lepiej nic nie sadź

27 kwi 23:48
kyrtap: ja te zadania co dałem robiłem w lutym więc nie pamiętam jak tam to leciało ale wiem że prawdo
było proste
27 kwi 23:48
Marcin: aa Tobie chodziło o podstawę

To nie, faktycznie się nie opłaca

27 kwi 23:49
Saizou : ktoś musi zalesiać tereny skoro Brazylijczycy wycinają "zielone płuca ziemi"
27 kwi 23:51
kyrtap: ale jednak zwrócę na te zadania dowodowe uwagę

27 kwi 23:51
zombi: Łatwa ta maturka, taka typowa, schematyczna. Masz coś jeszcze kyrtap?
27 kwi 23:53
kyrtap: nom mam chcecie arkusz 2?
27 kwi 23:55
Saizou : zombi mówiłem że dla ciebie to nic trudnego

27 kwi 23:56
zombi: Podaj ten arkusz drugi.
Saizou nie powiesz chyba, że tobie sprawiła problem...

27 kwi 23:58
kyrtap: dodam nowy post
27 kwi 23:59
kyrtap: dajcie z jakieś 10 min
27 kwi 23:59
Saizou : nie liczyłem całej, ale jak na te zadanka co robiłem to chciałbym mieć taką w maju

, albo
nie, wolę trudniejszą xd
27 kwi 23:59
zombi: Trudniejsza lepsza, większy rozrzut wyników będzie. I progi na studia niższe

28 kwi 00:02
Saizou : też tak pomyślałem xd
28 kwi 00:05
zombi: A fizyki nie zdaję, więc lepiej żeby ta matma była trudniejsza.

28 kwi 00:06
Saizou : a ja akurat fizykę zdaję jako sztuka dla sztuki, żeby w razie wypadku mieć choć jakieś
dodatkowe punkty
28 kwi 00:10
kyrtap: Saizou też podchodzisz do fizy? Ja niestety liczę na troszkę szczęścia

28 kwi 00:18
Saizou : a no tak jakoś wyszło, ale mam gwarancje że zdam fizykę

28 kwi 00:20
kyrtap: ale się przygotowywałeś do niej ?
28 kwi 00:21
Saizou : jeszcze nie

w sumie tylko to co na lekcjach
ja chcę zadanko z jednostek, takie matematyczne

28 kwi 00:22
kyrtap: ja też na to liczę i czytam same repetytorium a jaki poziom piszesz

28 kwi 00:28
Saizou : nieszczęsne rozszerzenie, ale jak juś się bawić to na całego

28 kwi 00:37
kyrtap: piona Saizou

28 kwi 00:44
kyrtap: 
28 kwi 00:44
kyrtap: jak zdam na 30% to będę uradowany choć jak przeglądam arkusze zawsze coś tam można policzyć
28 kwi 00:45
 ARKUSZ 1 (27 kwietnia rok 2014 godzina 16:13)
1. Zbadaj wzajemne położenie prostej określonej równaniem y = x +m i okręgu o równaniu
x2 + y2 = 9 w zależności od parametru m.
ARKUSZ 1 (27 kwietnia rok 2014 godzina 16:13)
1. Zbadaj wzajemne położenie prostej określonej równaniem y = x +m i okręgu o równaniu
x2 + y2 = 9 w zależności od parametru m.






 Ja miałem prawie 80
Ja miałem prawie 80 



 a gdzie mieszkasz, co?
a gdzie mieszkasz, co? 







 W przypadku wielomianów, gdzie dzielimy i ma wyjść 0 to jest super szybki sposób
W przypadku wielomianów, gdzie dzielimy i ma wyjść 0 to jest super szybki sposób 

 nie lubię za to grupowania
nie lubię za to grupowania 




 Mi to podzielenie hornerem zajęło dosłownie 30 sekund. Ja nie wiem gdzie
wy tutaj problem widzicie
Mi to podzielenie hornerem zajęło dosłownie 30 sekund. Ja nie wiem gdzie
wy tutaj problem widzicie

 ale coś o pierwiastkach zapewne
ale coś o pierwiastkach zapewne






 a teraz pasuje
a teraz pasuje 

 to był tylko rysunek poglądowy
to był tylko rysunek poglądowy 



 i się nie kłóćcie
i się nie kłóćcie 









 zaraz to zobaczę
zaraz to zobaczę 

 Chociaż nie powiem, są tu niektórzy mocno ogarniający
Chociaż nie powiem, są tu niektórzy mocno ogarniający 





 Według mnie tak
Według mnie tak  (w sensie przekrój)
(w sensie przekrój)
 zadania
zadania  1. Wyznacz zbiór wartości funkcji
f(x)= cosx√(1+tg2x)
oraz drugie
1. Wyznacz zbiór wartości funkcji
f(x)= cosx√(1+tg2x)
oraz drugie




 rozważałem inną opcję przez głupotę
rozważałem inną opcję przez głupotę 











 wynika to np. z tw. talesa
wynika to np. z tw. talesa

 Przekątne trapezu ABCD przecinają się w punkcie M. Wysokość trapezu ma długość 18. Pole
trójkąta ABM jest równe 25, pole trójkąta CDM jest równe 16. Oblicz pole trapezu.
P3=P4
Ptr=P1+P2+P3+P4 = P1+P2+2P3
Przekątne trapezu ABCD przecinają się w punkcie M. Wysokość trapezu ma długość 18. Pole
trójkąta ABM jest równe 25, pole trójkąta CDM jest równe 16. Oblicz pole trapezu.
P3=P4
Ptr=P1+P2+P3+P4 = P1+P2+2P3
 cos(45+22,5)=cos(67,5)
cos(45+22,5)=cos(67,5)


 Ew. można tak:
a=√2b
więc a+b = (√2+1)b
Z tw Pitagorasa policzyć c i wtedy.
Ale to taki drugi sposób, żeby był. Saizou lepszy.
Ew. można tak:
a=√2b
więc a+b = (√2+1)b
Z tw Pitagorasa policzyć c i wtedy.
Ale to taki drugi sposób, żeby był. Saizou lepszy.

 nie opłaca się moim zdaniem.
nie opłaca się moim zdaniem.


 ale już nie pamiętam, chyba z maja 2013 xd
w zadaniu 9 przyjemnie oznaczyć te wyrazy ciągu jako
a1=x−3r
a2=x−2r
a3=x−r
a4=x
a5=x+r
a6=x+2r
a7=x+3r
ale już nie pamiętam, chyba z maja 2013 xd
w zadaniu 9 przyjemnie oznaczyć te wyrazy ciągu jako
a1=x−3r
a2=x−2r
a3=x−r
a4=x
a5=x+r
a6=x+2r
a7=x+3r
 Bo ja chce wyniczki sprawdzać. W prawdo jak macie?
Tożsamość trygo łatwa.
Bo ja chce wyniczki sprawdzać. W prawdo jak macie?
Tożsamość trygo łatwa.
 Zad 10:
Ix−1I=2−Ix−3I
|x−5|≥3
x∊<1;2>
Lubię robić graficznie takie zadania, mam nadzieję, że jest ok
Zad 10:
Ix−1I=2−Ix−3I
|x−5|≥3
x∊<1;2>
Lubię robić graficznie takie zadania, mam nadzieję, że jest ok 




 zad. 6
zasadźmy drzewka
zad. 6
zasadźmy drzewka  W− wygrana
p− przegrana
n∊N+ i n≥6
W− wygrana
p− przegrana
n∊N+ i n≥6


 To nie, faktycznie się nie opłaca
To nie, faktycznie się nie opłaca 



 , albo
nie, wolę trudniejszą xd
, albo
nie, wolę trudniejszą xd




 w sumie tylko to co na lekcjach
ja chcę zadanko z jednostek, takie matematyczne
w sumie tylko to co na lekcjach
ja chcę zadanko z jednostek, takie matematyczne 



