ciagi Miko: Jak zbadać monotonicznośc takiego ciągu?

	⎧	1 dla n∊N i n≤7
an =	⎩	n dla n∊N i 8≤n≤15

Miko:

sushi_ gg6397228: zrób rysunek i potem powiedz co widzisz

Miko: jak to się przedstawia?

sushi_ gg6397228: n−−> oś pozioma a_n −−> oś pionowa nanosi się same punkty

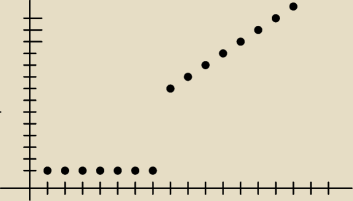
Miko: mniej wiecej cos takeigo

Dziadek Mróz: Ciąg jest swego rodzaju funkcją dyskretną, tzn. punktową, jak Miko pokazał

sushi_ gg6397228: i co teraz mozesz powiedziec o monotonicznosci ?

Dziadek Mróz: Co do układu równań, w edytorze jest możliwość rysowania układu i linii pomocniczych, klikamy ikonkę pod elipsą, jeżeli nie pojawi się układ przesuwamy kursorem i zaznaczamy poziom linii pomocniczych drugim klikiem

Miko: ze jest niemalejąca? i w takich przypadkach wystarczy sam wykres?

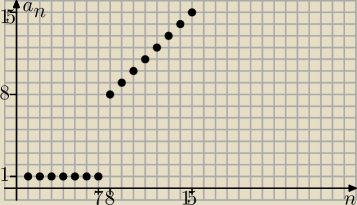
Dziadek Mróz: że jest stała w przedziale ... że jest rosnąca w przedziale ...

Dziadek Mróz: znaczy się on ciąg jest stały i rosnący