Funkcja wymierna Sebastian: Jeśli mógłby ktoś pomóc mi rozwiązać te zadania ... http://i58.tinypic.com/f4h2mu.png

bezendu: Nawet Ci się nie chcę przepisać ? Ja nie wchodzę w żadne linki

Marcin: Zapisz tutaj treść.

Tadeusz: liczba zadań jest mniejsza niżeli 17 ... więc też nie wchodzę −

zawodus: Skąd wiesz ile jest zadań jak nie wchodzisz?

Janek191:

	x − 8		(x + 3) − 11		− 11
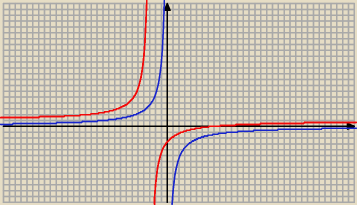
1) y =		=		= 1 +
	x + 3		x + 3		x + 3

	−11
Wykresy : g(x) =		− niebieski
	x

	− 11
f(x) =		+ 1 − czerwony
	x + 3

Sebastian: Nie chciało mi się przepisywać 3 raz tego samego, bo te zadania zamieściłem na 3 stronach i oczywiście każda miała inny kod, za którego pomocą zapisywało się ułamki itp. Dlatego nie mogłem po prostu skopiować, tylko musiałem za każdym razem pisać od nowa. Na 2 stronach pisałem od nowa, na trzeciej na szczęście była opcja dodawania załączników, więc dodałem to zdjęcie. Tutaj znowu inny kod i brak załączników, więc pomyślałem, że po prostu wkleję link... no ale mniejsza. 1. Zapisz wzór funkcji y = ^x−8_x+3 w postaci kanonicznej i naszkicuj jej wykres 2. Znajdź dziedzinę i zbiór wartości f(x) = ^3x−2_3x+6 oraz współrzędne, w których wykres tej funkcji przecina osie układu współrzędnych. 3. Rozwiąż równania: a) ^−x+12_x²−4x = 0 Tutaj normalny zapis bo trochę nie czytelnie to wygląda : −x+12/x do kwadratu −4x = 0 b) ³_x+2 = 2x + 3 4. Rozwiąż nierówności: a) ^3−4x_x+7 >3 b) ⁻⁵_6x−2 < lub równe ⁶_3−5x 5. Samochód przejechał 1/4 trasy ze średnią prędkością 80 km/h. Na całej trasie średnia prędkość samochodu była równa 64 km/h. Oblicz z jaką średnią prędkością samochód przejechał pozostałą część trasy.

Janek191:

	3 x − 2		(3x + 6) − 8		−8
2) f(x) =		=		= 1 +		=
	3 x + 6		3x + 6		3x + 6

	− 83
=		+ 1
	x + 2

więc Df = R \ { − 2} ZWf = R \ { 1 }

	3x − 2		2
f(x) = 0 ⇔		= 0 ⇔ 3x − 2 = 0 ⇔ x =
	3 x + 6		3

	2
A = (		; 0) − punkt przecięcia osi OX
	3

	0 −2		1
f(0) =		= −
	0 + 6		3

	1
B = ( 0; −		) − punkt przecięcia osi OY
	3

Janek191: 3)

	− x + 12
a)		= 0
	x2 − 4x

− x + 12
	= 0 ; x ≠ 0 i x ≠ 4
x*( x − 4)

− x + 12 = 0 x = 12 =====

	3
b)		= 2 x + 3 ; x ≠ − 2
	x + 2

3 = (2 x + 3)*( x + 2) 3 = 2 x² + 4x + 3x + 6 2 x² + 7 x + 3 = 0 Δ = 49 − 4*2*3 = 49 − 24 = 25 √Δ = 5

	− 7 − 5
x1 =		= − 3
	4

	− 7 + 5
x2 =		= − 0,5
	4

Marcin: 1.

x−8		x+3−11		−11
	⇒		⇒		+ 1
x+3		x+3		x+3

Marcin: ahh pierwsze już jest. Nie zauważyłem. Przepraszam

Sebastian: Dzięki, a mogliście by wytłumaczyć, jak dokładnie zostało zrobione to pierwsze ?. tzn. skąd wzięła się ta jedenastka ? Dodaję się licznik do mianownika, a potem sumę tego odejmuję się od licznika ?

Sebastian: I jeszcze w drugim zadaniu, skąd wzięła się ta 8 ?