równanie prostej przechodzącej przez dwa punkty
Ciekawska: Punkt A(9,0) i B(0,6) są wierzchołkami trójkąta prostokątnego ABC, ABC=90 stopni.
Przeciwprostokątna tego trójkąta zawiera się w osi OX. Napisz równania prostych zawierających
boki tego trójkata ABC.
Skorzystałam z tej strony:
https://matematykaszkolna.pl/strona/1223.html. I wychodzi mi tak:
(0−9)(y−0) = (6−)(x−9)
−9(y−0) = 6(x−9)
−9y = 6x − 9
−y = 6/9 − 1 → y= − 2/3 x + 1
O ile a przy x wyszło mi dobrze, to b już nie. Co zrobiłam źle?
27 kwi 13:22
ICSP: 6(x−9) = 6x − 54
27 kwi 13:25
Ciekawska: Aha, racja. Dziękuję

A jak policzyć C? Muszę najpierw narysować punkty A i B w układzie współrzędnych?
27 kwi 13:28
ICSP: Zrób rysunek, na pewno pomoże

27 kwi 13:29
Marcin:
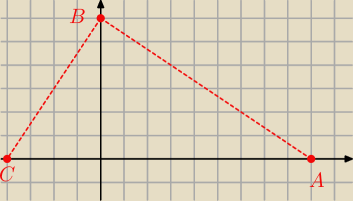

27 kwi 13:33
Ciekawska: A skąd wiadomo, że C ma współrzędne (4,0) ? Zero, to rozumiem, bo przeciwprostokątna miała
zawierać się w osi OX
Też podstawić? Np. AC
A(9,0) C(x2, 0)
27 kwi 13:39
ICSP: C(xc, 0 )
Co dalej ?
27 kwi 13:42
Marcin: Jak masz już równanie prostej AB, to piszesz teraz równanie prostej, która jest do niej
prostopadła i przechodzi przez punkt B. Tyle.
27 kwi 13:43
ICSP: albo liczysz długości odcinków |AB| , |BC| , |AC| i stosujesz twierdzenie Pitagorasa.
27 kwi 13:43
Ciekawska: Dalej będzie tak:
(xc − 9)(y − 0) = (0 − 0)(x − 9)
27 kwi 13:44
Marcin: Jak już masz równanie BC, to podstaw sobie za y=0 i wyliczysz x

27 kwi 13:45
Ciekawska: Nie ogarniam, mówiąc szczerze

.
27 kwi 13:46
Ciekawska: Marcin, okej

27 kwi 13:46
Ciekawska: Tylko, że dopiero mam zrobione równanie AB . I nie wiem, co zrobić, by wyliczyć x z C. (x2, 0)
27 kwi 13:48
Marcin: Jak masz AB, to wyznaczenie prostej prostopadłej do niej, przechodzącej przez B, to chyba nie
problem, co?

27 kwi 13:49
Ciekawska: A z Pitagorasa, to jak? Które wziąć współrzędne? Rozumiem, że BC oznaczyć jako b.
a2 + b2 = c,
czyli AB2 + BC2 = AC
27 kwi 13:50
Ciekawska: * AC2
27 kwi 13:51
Ciekawska: Marcin, właśnie nie wiem jak się za to zabrać.
27 kwi 13:52
Marcin: 0=3x+12
3x=−12
x=−4
C=(−4;0)
27 kwi 13:52
Ciekawska: A y policzyłeś w jaki sposób?
27 kwi 13:57
Marcin: Y to na pewno będzie 0

Bo to masz podane w treści zadania

27 kwi 13:58
Ciekawska: Tak, tak, ale chodzi mi o samo równanie.
y = 3/2 x + 6
27 kwi 14:01
Ciekawska: Odwróciłeś − 2/3x ?
27 kwi 14:01
5-latek: Ciekawska . A jakie wspolrzedne ma punkt przeciecia z osia OX i z osia OY (napisz tu ) chodzi
mi ogolnie
27 kwi 14:01
Marcin: Tak. Można powiedzieć że odwróciłem

27 kwi 14:04
Ciekawska: Punkt przecięcia z osią OX, czy miejsce zerowe. Wyznaczamy poprzez podstawienie liczb i
przyrównanie ich do zera, np. a − 2 = 0, wtedy a = 2
OY, gdy podstawiamy za x zero oraz wyliczamy y.
27 kwi 14:08
Ciekawska: * czyli
27 kwi 14:08
Ciekawska: OX −> (x1 , 0)
OY −> (0, f(0))
27 kwi 14:10
5-latek: No i fajnie

Teaz juz wiesz dlaczego y=0 dla punktu c?
27 kwi 14:12
Ciekawska: Tak, to wiedziałam cały czas

. Ale nie wiem, jak Marcin zrobił to równanie:
y = 3/2 x + 6
Chodzi mi o a przy x

.
27 kwi 14:13
Marcin: Żeby proste były prostopadłe, to ich współczynniki przy x, muszą spełniać coś takiego:
a
1 * a
2 = −1
Więc
27 kwi 14:18
Ciekawska: A, racja, dziękuję

. Jak się ma braki, to później tak jest.
27 kwi 14:22
Marcin: Jeszcze jest trochę czasu do matury, dasz radę

27 kwi 14:30
Ciekawska: Mam dwa lata

. A co do prostej AC, to:
(−4 − 9)(y−0) = (0−0)(x − 9)
− 13 y = 0
y = 0
Tak?

27 kwi 14:38
5-latek: tak
27 kwi 14:40
Marcin: A ja myślałem że jesteś tegoroczną maturzystką

Niepotrzebne to liczysz, bo przecież wiadomo, że ta prosta to y=0

27 kwi 14:41
Ciekawska: Nie, nie

. Robię zadania do specjalnego zeszytu. Za mną już 134 zadania, a pełna pula zadań z
tego rozdziału, to 260. Tak więc trochę roboty jest, a jutro w dodatku mam z tego sprawdzian
−> z zadań ze zbioru.
Jakieś rady?

27 kwi 14:44
Marcin: Nie stresuj się, taka rada

27 kwi 14:45
Ciekawska: W szkole się prawie nigdy nie stresuję

.
27 kwi 14:48
Ciekawska:
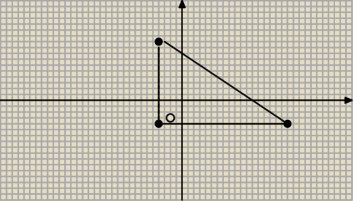
A zadanie podobne:
Przyprostokątne trójkąta prostokątnego ABC zawierają się w prostych równoległych do osi ukladu
współrzędnych. wyznacz równania prostych zawierających boki tego trójkata jesli B(−2,5)
C(10,−1).
Skoro równoległe, to a
1 = a
2
Mam to zrobić tak jak wcześniejsze zadanie?
27 kwi 14:59
Marcin:
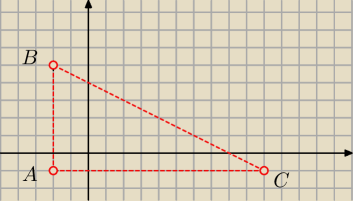
AC ⇒ y=−1
BA ⇒ x=−2
A=(−2;−1)
27 kwi 15:19
Ciekawska: Dziękuję

A wytłumaczyłbyś mi jeszcze raz jak wylicza się punkt, którego się nie ma? Proszę, bo nie
rozumiem tego dalej

.
27 kwi 16:13
 A jak policzyć C? Muszę najpierw narysować punkty A i B w układzie współrzędnych?
A jak policzyć C? Muszę najpierw narysować punkty A i B w układzie współrzędnych?




 .
.


 Bo to masz podane w treści zadania
Bo to masz podane w treści zadania 

 Teaz juz wiesz dlaczego y=0 dla punktu c?
Teaz juz wiesz dlaczego y=0 dla punktu c?
 . Ale nie wiem, jak Marcin zrobił to równanie:
y = 3/2 x + 6
Chodzi mi o a przy x
. Ale nie wiem, jak Marcin zrobił to równanie:
y = 3/2 x + 6
Chodzi mi o a przy x  .
.

 . Jak się ma braki, to później tak jest.
. Jak się ma braki, to później tak jest.

 . A co do prostej AC, to:
(−4 − 9)(y−0) = (0−0)(x − 9)
− 13 y = 0
y = 0
Tak?
. A co do prostej AC, to:
(−4 − 9)(y−0) = (0−0)(x − 9)
− 13 y = 0
y = 0
Tak? 
 Niepotrzebne to liczysz, bo przecież wiadomo, że ta prosta to y=0
Niepotrzebne to liczysz, bo przecież wiadomo, że ta prosta to y=0 
 . Robię zadania do specjalnego zeszytu. Za mną już 134 zadania, a pełna pula zadań z
tego rozdziału, to 260. Tak więc trochę roboty jest, a jutro w dodatku mam z tego sprawdzian
−> z zadań ze zbioru.
Jakieś rady?
. Robię zadania do specjalnego zeszytu. Za mną już 134 zadania, a pełna pula zadań z
tego rozdziału, to 260. Tak więc trochę roboty jest, a jutro w dodatku mam z tego sprawdzian
−> z zadań ze zbioru.
Jakieś rady? 

 .
.
 A zadanie podobne:
Przyprostokątne trójkąta prostokątnego ABC zawierają się w prostych równoległych do osi ukladu
współrzędnych. wyznacz równania prostych zawierających boki tego trójkata jesli B(−2,5)
C(10,−1).
Skoro równoległe, to a1 = a2
Mam to zrobić tak jak wcześniejsze zadanie?
A zadanie podobne:
Przyprostokątne trójkąta prostokątnego ABC zawierają się w prostych równoległych do osi ukladu
współrzędnych. wyznacz równania prostych zawierających boki tego trójkata jesli B(−2,5)
C(10,−1).
Skoro równoległe, to a1 = a2
Mam to zrobić tak jak wcześniejsze zadanie?
 AC ⇒ y=−1
BA ⇒ x=−2
A=(−2;−1)
AC ⇒ y=−1
BA ⇒ x=−2
A=(−2;−1)
 A wytłumaczyłbyś mi jeszcze raz jak wylicza się punkt, którego się nie ma? Proszę, bo nie
rozumiem tego dalej
A wytłumaczyłbyś mi jeszcze raz jak wylicza się punkt, którego się nie ma? Proszę, bo nie
rozumiem tego dalej  .
.