kombinatoryka tyu: czy ktoś mógłby wyjaśnić mi to zadanie, bo znalazłem tylko takie zdawkowe rozwiązanie? Ze zbioru {1,2,...,50} losujemy ze zwracaniem kolejno dwie liczby. Oznaczamy je (w kolejności losowania) a oraz b. Ile jest takich par (a, b), dla których liczba |a−b| jest podzielna przez 4. Odp. liczba |a−b| jest podzielna przez 4, jeśli liczby a i b dają te same reszty z dzielenia przez 4. 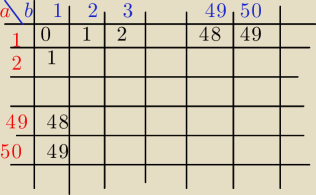Wśród tych liczb jest: − 12 liczb podzielnych przez 4 − 13 liczb dających resztę 1 − 13 liczb dających resztę 2 − 12 liczb dających resztę 3 szukanych par jest więc: 12²+13²+13²+12²=2⋅144+2⋅169=626 Czarnym kolorem jest wynik Ia−bI Liczyłem sobie na kartce i wyszło mi, że w zbiorze {1,2,..,50} jest 12 liczb podzielnych przez 4, czyli 4,8,12, 16,20, 24, 28, 32, 36, 40, 44, 49. Ale nie wiem co dalej.

tyu: ostatnia liczba to 48 zamiast 49