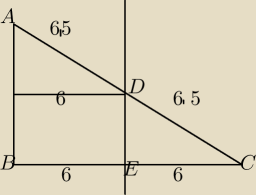
do sprawdzenia abc+d: Hej mam takie zadanko. Dany jest trójkąt prostokątny o przeciwprostokątnej długości 13 cm i jednej z przyprostokątnych długości 5 cm. Trójkąt ten podzielono prostą prostopadłą do dłuższej przyprostokątnej i przechodzącej przez jej środek. Oblicz pola figur powstałych w wyniku podziału trójkąta tą prostą. Ja rozwiązałem to na takiej zasadzie, że napisałem komentarz, że skoro prosta DE przecina przyprostokątną BC w połowie pod kątem prostym to przeciwprostokątną AC również przecina w połowie. Dalej już poleciało z Pitagorasa, aby wyznaczyć DE. Wyniki mam identyczne jak w odpowiedziach. Jednak chciałbym się spytać, czy takie rozwiązanie miałoby pełną punktację, gdyż w odpowiedziach jest to rozwiązane za zasadzie podobieństwa trójkątów. Z góry dziękuję za odpowiedź>

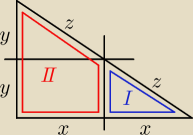Dziadek Mróz: x = ? 2y = 5 y = 2.5 2z = 13 z = 6.5 (2y)² + (2x)² = (2z)² 4y² + 4x² = 4z² y² + x² = z² x² = z² − y² x = √z² − y² x = √6.5² − 2.5² = √42.25 + 6.25 = √48.5 = 6.96 ≈ 7

	x * y
PI =
	2

	(2y+y)*x
PII =
	2

abc+d: No ok tak właśnie zrobiłem, ale bardziej mi chodzi o to czy mogę tak od razu sobie zapisać , że ta prosta podzieli przeciwporstokątną na połowy

abc+d: Zresztą ty to źle zrobiłeś bo x jest równy 6. xd bo z całego trójkąta 4x²=169−25=144 x²=36 −> x=6

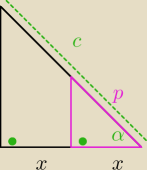zombi: Zawsze można to udowodnić, że dzieli na połowy. Np. z trójkątów podobnych: Trójkąty mniejszy (fioletowy) oraz duży są podobne z cechy (kkk) Zatem zachodzą proporcje

p		c
	=		/*2x
x		2x

⇔

	1
2p = c ⇔ p =		c
	2