Dla maturzystów Domel: Dla maturzystów Dany jest kąt ostry oraz punkt A leżący wewnątrz tego kąta. Na ramionach kąta znaleźć takie punkty B i C, aby obwód trójkąta ABC był możliwie najmniejszy.

Saizou : Domel nie za bardzo wiem czego od nas wymagasz, znaczy się, jak chcesz określić te B,C ? jako co ?

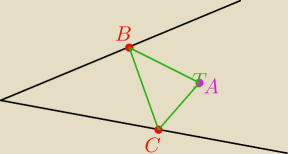
Domel: Taki przykładowy szkic − ale jak wyznaczyć B i C, żeby obwód trójkąta był najmniejszy

Domel: Kiedyś na forum było zadanko, że mamy dwa punkty A i B leżące po jednej stronie osi X i znaleźć na tej osi X punkt C taki, że suma odległości |AC| i |BC| jest najmniejsza − tutaj trzeba spróbować podejść analogicznie

Saizou : ale nie wiem nadal o co ci chodzi, jak chcesz określić położenie punktów, w sensie ileś tam odległości od wierzchołka kąta ?

Domel: Nie chodzi o obliczenie odległości analitycznie (zwłaszcza od wierzchołka kąta) − to zadanie trzeba rozwiązać graficznie i logicznie

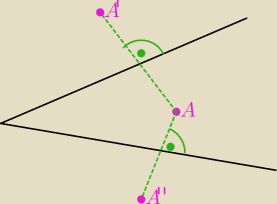
Domel: Może to coś pomoże i nastąpi światłość (oby nie zaciemniło ) No to gdzie (graficznie) powinny leżeć punkty B i C, żeby obwód trójkąta był najmniejszy?

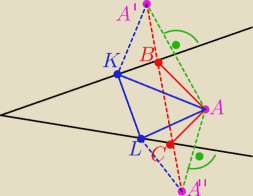
Domel: No dobra − zauważ, że obwód trójkąta to: Ob. = |AB| + |AC| + |BC| ∧ Ob. = |A'B| + |A''C| + |BC| Obwód trójkąta będzie najmniejszy, jeżeli punkty B i C będą leżeć na prostej A'A'' (|A'B| = |AB| i |A''C| = |AC|) Zauważ, że np. obwód trójkąta AKL > od obwodu trójkąta ABC bo K i L nie leżą na prostej A'A'' (punkty A' i A'' łączą łamane odcinki przez K i L) więc trójkąt AKL nie będzie miał najmniejszego obwodu

Domel: Odkopałem to zadanie na kamiennych tablicach z lat 80−tych zamierzchłego wieku